5  感度解析

入力パラメタに対する出力パラメタの感度の問題には以下のようなものがある。 (Talagrand 1991).

感度実験（sensitivity experiments）
入力パラメタの変化に対する系の物理応答を調べる。
不確実性の定量化（Uncertainty quantification）
入力パラメタの不確実性により生じる出力パラメタの不確実性を測る。
感度解析（sensitivity analysis）
モデルの入力パラメタの何が、出力パラメタにおいて後験的に観測された、特徴の源であったのかを特定する。
パラメタ推定（parameter estimation）及びデータ同化（data assimilation）
出力パラメタが与えた条件を満たすような入力パラメタの値を求める。

予報感度解析は予報に含まれる特徴の源を見つける手法で、ターゲット観測に応用されてきた (Snyder 1996; Lorenz and Emanuel 1998; Bishop and Toth 1999)。 感度は、予報モデルの随伴(Rabier et al. 1996; Langland et al. 2000) やアンサンブル予報 (Ancell and Hakim 2007; Enomoto et al. 2007)から計算できるが、ラグランジュの未定乗数法を用いると一貫した導出が可能である(Enomoto et al. 2015)。

5.1 摂動の線型成長

初期\(t=0\)における状態\(\mathbf{x}_0\)からの非線型時間発展を考える。

\[ \mathbf{x}_\tau=M(\mathbf{x}_0) \tag{5.1}\]

初期摂動 \(\mathbf{y}\) 次の式に従って線型に成長するものと仮定し、 時刻 \(\tau\) での摂動を \(\mathbf{z}\) で表す。

\[ \mathbf{z} = M(\mathbf{x}_0 + \mathbf{y}) - M(\mathbf{x}_0)\approx \mathbf{My} \tag{5.2}\]

ここで \(\mathbf{M} = \partial M/\partial \mathbf{x}\) は接線型モデルである。

5.2 随伴感度

\(\|\mathbf{y}\|\equiv\sqrt{\mathbf{y}^\mathrm{T}\mathbf{G}_0\mathbf{y}}=1\)という条件の下で、\(\delta J\) を最大にする \(\mathbf{y}\) を求める。

\[ F(\mathbf{y}, \lambda) = \delta J + \lambda(1 - \mathbf{y}^\mathrm{T}\mathbf{G}_0\mathbf{y}) \]

を最小化する。ここで、 \(\lambda\) はラグランジュの未定乗数で \(\delta J\) 　は

\[ \begin{aligned} \delta J = \left[\frac{\partial J}{\partial\mathbf{x}_\tau}\right]^\mathrm{T}\mathbf{z} = \left[\frac{\partial J}{\partial\mathbf{x}_\tau}\right]^\mathrm{T}\mathbf{M}\mathbf{y} = \left[\mathbf{M}^\mathrm{T}\frac{\partial J}{\partial\mathbf{x}_\tau}\right]^\mathrm{T}\mathbf{y} =\left[\frac{\partial J}{\partial\mathbf{x}_0}\right]^\mathrm{T}\mathbf{y} \end{aligned} \tag{5.3}\] で表される。

つまり、

\[ F(\mathbf{y}, \lambda) = \left[\frac{\partial J}{\partial\mathbf{x}_0}\right]^\mathrm{T}\mathbf{y} + \lambda(1 - \mathbf{y}^\mathrm{T}\mathbf{G}_0\mathbf{y}) \]

\(\partial F/\partial\mathbf{y}=0\) を計算すると

\[ 2\lambda\mathbf{y} = \mathbf{G}_0^{-1}\mathbf{M}^\mathrm{T}\frac{\partial J}{\partial \mathbf{x}_\tau} = \mathbf{G}_0^{-1}\frac{\partial J}{\partial \mathbf{x}_0}. \tag{5.4}\]

が得られる。

5.3 特異ベクトル感度

特異ベクトル（SV: singular vector）感度は \(\|\mathbf{y}\|=1\) の条件の下で \(\|\mathbf{z}\|\equiv\sqrt{\mathbf{z}^\mathrm{T}\mathbf{G}_\tau\mathbf{z}}\) を最大化する \(\mathbf{y}\) を求めるには、

\[ F(\mathbf{y}, \lambda) = \mathbf{z}^\mathrm{T}\mathbf{G}_\tau\mathbf{z} + \lambda(1 - \mathbf{y}^\mathrm{T}\mathbf{G}_0\mathbf{y}) \]

を最小化する。 \(\partial F/\partial\mathbf{y} = 0\) を計算すると一般化固有値問題

\[ \mathbf{M}^\mathrm{T}\mathbf{G}_\tau\mathbf{M}\mathbf{y} = \lambda\mathbf{G}_0\mathbf{y}. \tag{5.5}\]

が得られる。 左から \(\mathbf{y}^\mathrm{T}\) を掛けると、

\[ \lambda = \|\mathbf{z}\|^2/\|\mathbf{y}\|^2 \tag{5.6}\]

つまり成長率の二乗となる。 \(n\times n\)の\(\mathbf{G}_0\) 及び \(\mathbf{G}_0^{-1}\mathbf{M}^\mathrm{T}\mathbf{G}_\tau\mathbf{M}\)の逆行列を計算する必要がある。

5.4 アンサンブル随伴感度解析

\(\mathbf{p}\) で重みづけした平均で最適な摂動を \(\mathbf{y} = \mathbf{Yp}\) 及び \(\delta J = \boldsymbol\delta\mathbf{J}^\mathrm{T}\mathbf{p}\) と表す。 ここで \(\mathbf{Y} = (\mathbf{y}_1,\,\mathbf{y}_2,\dots,\mathbf{y}_m)^\mathrm{T}\) 及び \(\boldsymbol\delta\mathbf{J} = (\delta J_1,\,\delta J_2,\dots,\delta J_m)^\mathrm{T}\)である。 \(\|\mathbf{y}\|=1\)の条件下で \(\delta J\) を最大化する \(\mathbf{p}\) を求めるには、

\[F(\mathbf{p}, \lambda) = \boldsymbol\delta\mathbf{J}^\mathrm{T}\mathbf{p} + \lambda(1 - \mathbf{p}^\mathrm{T}\mathbf{Y}^\mathrm{T}\mathbf{G}_0\mathbf{Yp}) \]

を最小化すればよい。 \(\partial F/\partial\mathbf{p} = 0\) を計算すると

\[ 2\lambda\mathbf{p} = (\mathbf{Y}^\mathrm{T}\mathbf{G}_0\mathbf{Y})^{-1}\boldsymbol\delta\mathbf{J} \]

すなわち

\[ \mathbf{y} \propto\mathbf{Y}(\mathbf{Y}^\mathrm{T}\mathbf{G}_0\mathbf{Y})^{-1}\boldsymbol\delta\mathbf{J} \]

を得る。 \(\|\mathbf{y}\|_i=1\) かつ \(\mathbf{y}_i^\mathrm{T}\mathbf{G}_0\mathbf{y}_j = 0,\;i\ne j\) ならば \(\mathbf{Y}^\mathrm{T}\mathbf{G}_0\mathbf{Y} \propto \mathbf{I}\) 及び \(\mathbf{y} = \mathbf{Y}\boldsymbol\delta\mathbf{J}\)。

Note

  • \(\partial J/\partial \mathbf{x}_t = 2 \mathbf{G}_t \mathbf{z}\) なら、Equation 5.6 同様に指数函数的成長を示唆する。

  • メンバ数が状態数に近づく（\(m\rightarrow n\)） につれて、アンサンブル随伴感度は随伴感度に漸近する。

5.5 単回帰

各アンサンブルメンバが \(\delta J = [\partial J/\partial \mathbf{x}_0]^\mathrm{T}\mathbf{y}\) であるとき、これを集めて \(\boldsymbol\delta\mathbf{J} = \mathbf{Y}^\mathrm{T}\partial J/\partial \mathbf{x}_0\) と表す。

左から \(\mathbf{Y}\) を掛けると最小分散解 \[\frac{\partial J}{\partial\mathbf{x}_0} = (\mathbf{YY}^\mathrm{T})^{-1}\mathbf{Y}\boldsymbol\delta\mathbf{J} \tag{5.7}\]

Ancell and Hakim (2007) はさらに \(\mathbf{A}=\mathbf{YY}^\mathrm{T}\) に対して対角近似 \(\mathbf{D}=\mathrm{diag}(\mathbf{A})\) を仮定し、単回帰を得た。

5.6 多変数回帰

Hacker and Lei (2015) は感度解析を次のように定式化した。

\[ \delta\mathbf{J} = \mathbf{Y}^\mathrm{T}\boldsymbol{\beta} + \boldsymbol{\varepsilon} \tag{5.8}\]

を考えた。ここで\(\boldsymbol{\beta} = \partial J/\partial \mathbf{x}_0\)である。 状態の自由度が標本数よりも大きい場合、Equation 5.8は劣決定となる。

解を一つに定めるため最小ノルム解を考え、\(\delta\mathbf{J} = \mathbf{Y}^\mathrm{T}\boldsymbol{\beta}\) の条件の下で \(\boldsymbol{\beta}^\mathrm{T}\boldsymbol{\beta}\) を最小化した。

\[\frac{\partial J}{\partial \mathbf{x}_0} = \mathbf{Y}(\mathbf{Y}^\mathrm{T}\mathbf{Y})^{-1}\boldsymbol\delta\mathbf{J}\] これは多変数回帰である。

Duc et al. (2023) は正則化とMoore–Penrose逆行列を用いて主双対解を得た。 Enomoto et al. (2015) は多変量で、アンサンブル空間で逆行列を求めており、初期ノルム \(\mathbf{G}_0\) を考慮している。

5.7 アンサンブルSV

重み \(\mathbf{p}\) を用いて検証時刻の摂動を \(\mathbf{z} = \mathbf{Zp}\) 表す。 \(\|\mathbf{y}\|=1\) の下で \(\mathbf{p}^\mathrm{T}\mathbf{Z}^\mathrm{T}\mathbf{G}_\tau\mathbf{Zp}\) を最大化する\(\mathbf{p}\) を求める。

\[F(\mathbf{p}, \lambda) = \mathbf{p}^\mathrm{T}\mathbf{Z}^\mathrm{T}\mathbf{G}_\tau\mathbf{Z}\mathbf{p} + \lambda(1 - \mathbf{p}^\mathrm{T}\mathbf{Y}^\mathrm{T}\mathbf{G}_0\mathbf{Y}\mathbf{p})\]

を最小化する。 \(\partial F/\partial\mathbf{p} = 0\) を計算し、一般化固有値問題 \[ \mathbf{Z}^\mathrm{T}\mathbf{G}_\tau\mathbf{Zp} = \boldsymbol\Lambda \mathbf{Y}^\mathrm{T}\mathbf{G}_0\mathbf{Yp}. \] を得る。 \(\mathbf{Y}^\mathrm{T}\mathbf{G}_0\mathbf{Y}\propto\mathbf{I}\) なら \(\mathbf{Z}^\mathrm{T}\mathbf{G}_\tau\mathbf{Zp} = \boldsymbol\Lambda\mathbf{p}\) に帰着する。 アンサンブル変換（ET: ensemble transform）　(Bishop and Toth 1999) 及び解析誤差共分散SV (Hamill et al. 2003) と同じである。

5.8 日本域に対するアンサンブル感度

Enomoto, Yamane, Ohfuchi (2015)

  • データ: 25メンバの気象庁週間アンサンブル予報
  • 初期時刻: 2003年1月2日1200 UTC
  • 検証領域: 125\(^\circ\)N–150\(^\circ\)E, 25°N–50°N
  • 検証時刻: 2003年1月5日1200 UTC
  • 乾燥全エネルギノルム \(\mathrm{TE} = \frac{1}{2}\int_{p_\mathrm{r}}^{p_\mathrm{t}}\int_A u^{'2} + v^{'2} + \frac{c_p}{T_\mathrm{r}}T^{'2}+RT_\mathrm{r}\left(\frac{p_\mathrm{s}'}{p_\mathrm{r}}\right)^2\mathrm{d}A\mathrm{d}p\)

5.9 2003年3月の爆弾低気圧

Enomoto, Yamane, Ohfuchi (2015)

左列: 2003年1月23日及び24日9時（日本時）の気象庁天気図。右2列: 1月21日1200 UTCからの気象庁週間アンサンブル予報を用いたアンサンブル感度解析（上段、左からEnSVSA及びEnASA）、初期及び　検証時刻のアンサンブルスプレッド。検証領域を矩形で示す。

5.10 乾燥全エネルギノルムの時間発展

Enomoto, Yamane, Ohfuchi (2015)

乾燥全エネルギノルムの時間発展。2003年1月2日1200 UTCからの気象庁週間アンサンブル予報。検証領域は日本域（120°—150°E、20°N—50°N）。横軸は予報時間（h）、縦軸は鉛直に積算した単位面積あたりの乾燥全エネルギノルム。細実線はアンサンブルメンバ、太実線はアンサンブル平均、破線は予報時間72 hに対するアンサンブル特異ベクトル第一モード。\(\circ\)は各予報時間に対する第一モード

5.11 欧州の切離低気圧と熱帯低気圧 Cristobal 2002

Enomoto, Ohfuchi, Nakamura, Shapiro (2007)

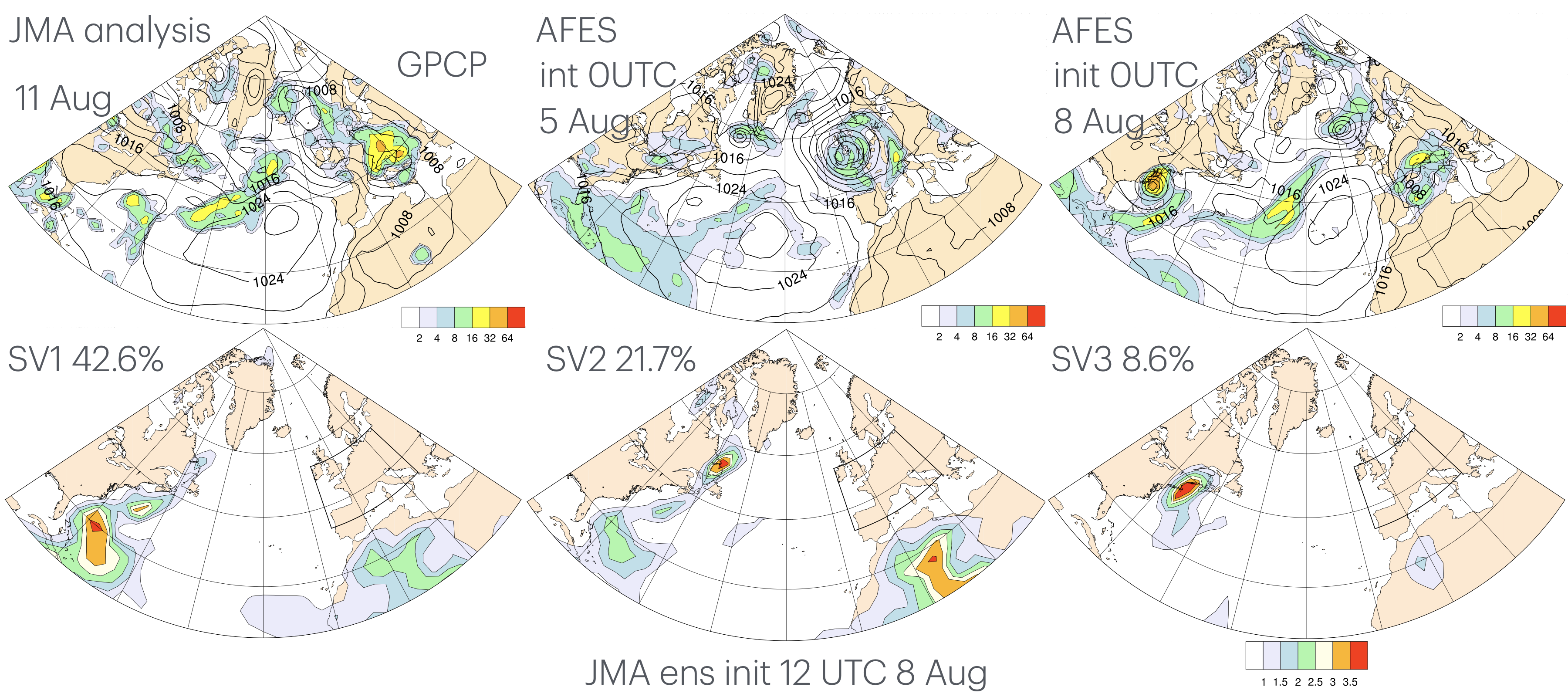
上段: 2002年8月11日0000UTCにおける気象庁海面気圧解析 hPa 及びGPCP降水量 mm/d（左）、AFESによる8月5日（中）及び8日（右）0000UTCからの予報。下段: 8月8日1200 UTCからの気象庁アンサンブル予報を用いたアンサンブル特異ベクトル第一〜三（右から左）, Enomoto et al. 2007

5.12 アンサンブル SV の適用例

  • Nishii and Nakamura (2010) は2006年1月下旬の成層圏突然昇温は北大西洋のブロッキングに感度があり、ブロッキングは北東太平洋の低気圧に感度があることを見出した。
  • Matsueda et al. (2011) は 2005年12月15日のNCEP の予報が外れ、ブロッキングが強すぎた原因は中部北東太平洋の不確実性にあると特定した。
  • Takemura et al. (2021) はモンスーントラフの予報に影響を与えた、上流の気圧の峰と下流の渦位偏差を検出した。

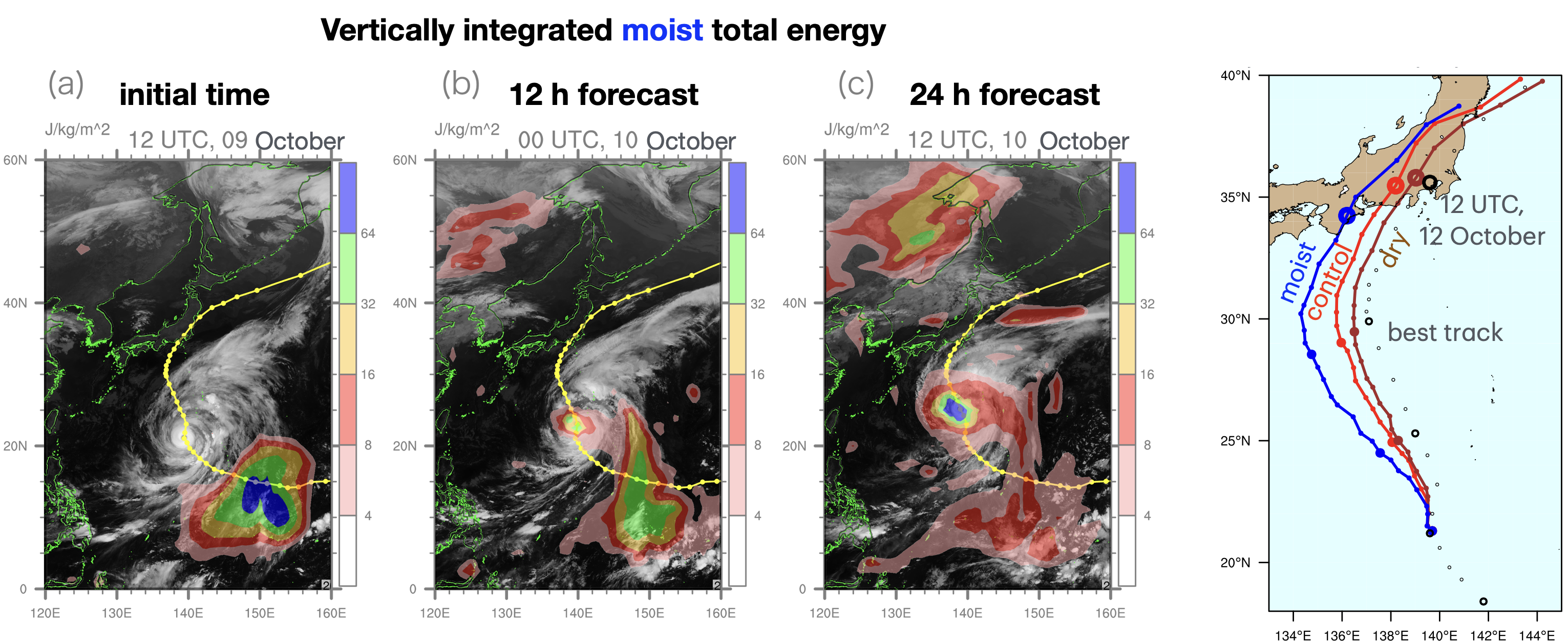
5.13 台風Hagibis 2019

Nakashita and Enomoto (2021)

左: 鉛直に積分された湿潤全エネルギで示された感度。左から初期時刻、12時間予報、24時間予報）（Nakashita and Enomoto (2021), Fig. 4にひまわり画像を追加）、右: 気象庁GSMを用いて摂動を加えた実験（中下他 2025, 気象研究ノート249

5.14 まとめ

  • 予報感度解析は注目している現象に影響を与える領域や変数を特定する有用な道具である。
  • 随伴及びアンサンブルに基づく定式化は、どちらもラグランジュの未定乗数法で一貫して導出できる。
  • アンサンブルSVは、爆弾低気圧や台風など顕著な気象に適用され、メカニズムや予測可能性に関する要因を特定できただけでなく、アンサンブルカルマンフィルタのインフレーションとして有効である。
  • 偽りの感度は局所化等を用いて特定する必要がある。 (Griewank et al. 2023).