基礎方程式系
この節では安定性問題を取り扱うために便利な基礎方程式系を対数気圧座標で表し,準地衡風近似の下での渦位方程式を導出する。
対数気圧座標
傾圧不安定問題では,対数気圧座標
\[z^* = -H\ln\frac{p}{p_\mathrm{ref}}\]
を用いると便利である。ここで\(p_\mathrm{ref}\)は参照気圧,
\[H = \frac{RT_\mathrm{ref}}{g}\]
は参照気温\(T_\mathrm{ref}\)を用いたスケールハイトである。
\(z^*\)は\(p\)のみの函数なので,
\[\left(\frac{\partial}{\partial t}\right)_p = \left(\frac{\partial}{\partial t}\right)_{z^*},\; \nabla_p=\nabla_{z^*}\]
である。また
\[\begin{aligned}
\frac{\partial}{\partial p} & = -\frac{H}{p}\frac{\partial}{\partial z^*}, \\
\omega &= -\frac{p}{H}w^*,\; w^* \equiv \frac{\mathrm{d}z^*}{\mathrm{d}t}
\end{aligned}\]
より,
\[\frac{\mathrm{d}}{\mathrm{d}t} = \frac{\partial}{\partial t} + \pmb{v}\cdot\nabla + w^*\frac{\partial}{\partial z^*}\]
となる。
運動方程式
\[\frac{\mathrm{d}\pmb{v}}{\mathrm{d}t}+f\pmb{k}\times\pmb{v}=-g\nabla z\]
熱力学の式
\[\frac{\mathrm{d}\ln\theta}{\mathrm{d}t} = \frac{\dot{Q}}{c_pT}\]
は\(p\)座標のEquation 2.1, Equation 2.2と同形である。
静力学平衡
\[\frac{\partial\phi}{\partial z^*} = \frac{RT}{H}\]
連続の式
\[\nabla\cdot\pmb{v}+\frac{\partial w^*}{\partial z^*}-\frac{w^*}{H}=0 \tag{3.1}\]
は
\[\rho_0 \equiv \rho_{\mathrm{ref}}\exp\left(-\frac{z^*}{H}\right)\]
を用いると,
\[\nabla\cdot\pmb{v}+\frac{1}{\rho_0}\frac{\partial(\rho_0w^*)}{\partial z^*}=0 \tag{3.2}\]
とも書ける。
準地衡渦位方程式
\(z^*\)座標での運動方程式は
\[\frac{\mathrm{d}_\mathrm{g}u_\mathrm{g}}{\mathrm{d}t} = f_0v_\mathrm{a}+\beta yv_\mathrm{g}\]
\[\frac{\mathrm{d}_\mathrm{g}v_\mathrm{g}}{\mathrm{d}t} =-f_0u_\mathrm{a}-\beta yu_\mathrm{g}\]
であり\(p\)座標のEquation 2.4, Equation 2.5と同形である。
非地衡風成分の連続の式は,\(p\)座標系Equation 2.8の
\[\nabla \cdot \pmb{v}_\mathrm{g} = 0\]
\[\nabla \cdot \pmb{v}_\mathrm{a}+\frac{\partial\omega}{\partial p} = 0\]
及びEquation 3.2より
\[\nabla\cdot\pmb{v}_\mathrm{a}+\frac{1}{\rho_0}\frac{\partial(\rho_0w^*)}{\partial z^*}=0 \tag{3.3}\]
となる。
熱力学の式は,\(p\)座標系における\(T\)で表したEquation 2.10
\[\frac{\mathrm{d}_\mathrm{g}T}{\mathrm{d}t} -\frac{p}{R}S_0\omega = \frac{\dot{Q}}{c_p}\]
より
\[\frac{\mathrm{d}_\mathrm{g}}{\mathrm{d}t}\left(\frac{\partial\phi}{\partial z^*}\right)+N^{*2}w^* = \frac{\kappa\dot{Q}}{H} \tag{3.4}\]
と書ける。 ここで,
\[N^{*2} \equiv \frac{R}{H}\left(\frac{\partial T}{\partial z^*}+\frac{\kappa T}{H}\right) = \left(\frac{p}{H}\right)^2S_0\]
\(\kappa = R/c_p\)である。
\(\partial\)Equation 2.5\(/\partial x-\partial\)Equation 2.4\(/\partial y\)より,準地衡渦度方程式
\[\frac{\mathrm{d}_\mathrm{g}\zeta_\mathrm{g}}{\mathrm{d}t} = \frac{f_0}{\rho_0}\frac{\partial(\rho_0 w^*)}{\partial z^*} - \beta v_g \tag{3.5}\]
が得られる。ここで連続の式Equation 2.8, Equation 3.3を用いた。
断熱(\(\dot{Q}=0\))のとき,Equation 3.5 とEquation 3.4から\(w^*\)を消去すると,
\[\frac{\mathrm{d}_\mathrm{g}q}{\mathrm{d}t}=0 \tag{3.6}\]
ここで\(q\)は,準地衡渦位
\[q = f_0 + \beta y + \nabla^2\psi + \frac{1}{\rho_0}\frac{\partial}{\partial z^*}\left(\epsilon\rho_0\frac{\partial\psi}{\partial z^*}\right),\;\epsilon = \frac{f_0^2}{N^{*2}}\]
である。非粘性,断熱の場合,\(q\)は保存する。
線型安定性問題
準地衡流線函数\(\psi\)を東西一様で定常な基本場と擾乱とに分ける。
\[\psi(x,y,z^*,t) = \overline{\psi}(y,z^*) + \psi'(x,y,z^*,t)\]
擾乱は微小\(\psi \ll 1\)であるとし,2次の項は無視する。 Equation 3.6を線型化すると
\[\left(\frac{\partial}{\partial t}+\overline{u}\frac{\partial}{\partial x}\right)q'+\frac{\partial\overline{q}}{\partial y}\frac{\partial\psi'}{\partial x} = 0 \tag{3.7}\]
となる。ここで,基本場は
\[\overline{u} = \overline{u}(y,z^*)\]
のみとする。また,
\[q' = \nabla^2\psi' + \frac{1}{\rho_0}\frac{\partial}{\partial z^*}\left(\epsilon\rho_0\frac{\partial\psi'}{\partial z^*}\right) \tag{3.8}\]
は渦位擾乱,
\[\frac{\partial\overline{q}}{\partial y} = \beta - \frac{\partial^2\overline{u}}{\partial y^2} - \frac{1}{\rho_0}\frac{\partial}{\partial z^*}\left(\epsilon\rho_0\frac{\partial\overline{u}}{\partial z^*}\right) \tag{3.9}\]
は基本場の南北渦位勾配である。
南北の境界\(y=\pm L\)で
\[v' = \frac{\partial\psi'}{\partial x} = 0,\; \psi' = 0,\]
という側面境界条件を与える。上下端で\(w^* = 0\)とし熱力学の式Equation 3.4より
\[\left(\frac{\partial}{\partial t} + \overline{u}\frac{\partial}{\partial x}\right)\frac{\partial\psi'}{\partial z^*} - \frac{\partial\overline{u}}{\partial z^*}\frac{\partial\psi'}{\partial x} = 0 \tag{3.10}\]
が境界条件となる。
線型安定性問題では,無限小振幅の擾乱に対する基本場\(\overline{u}(y,z^*)\)の安定性を調べる。流れが不安定で擾乱が成長すると,最終的には非線型効果が無視できなくなる。流れが安定でも,有限振幅の擾乱に対しては不安定となる可能性がある。
不安定の必要条件
Equation 3.7に\(\rho_0\psi'\)をかけて空間積分すると,
\[\frac{\partial E'(\psi')}{\partial t} = \int\int\rho_0\left[\overline{\frac{\partial\psi'}{\partial x}\frac{\partial\psi'}{\partial y}}\frac{\partial\overline{u}}{\partial y} +\epsilon\overline{\frac{\partial\psi'}{\partial x}\frac{\partial\psi'}{\partial z^*}}\frac{\partial\overline{u}}{\partial z}\right]\mathrm{d} y \mathrm{d} z^*\]
となる。ここで
\[E'(\psi') = \int\int\ \frac{\rho_0}{2}\left[\overline{\left(\frac{\partial\psi'}{\partial x}\right)^2+\left(\frac{\partial\psi'}{\partial y}\right)^2+\epsilon\left(\frac{\partial\psi'}{\partial z^*}\right)^2}\right]\mathrm{d} y \mathrm{d} z^*\]
は擾乱の全エネルギーである。
右辺第1項は,レイノルズ応力\(-\rho_0\overline{v'u'}\)と基本東西風の南北シアとの積で擾乱のエネルギーが生じることを示す。この過程を順圧不安定(barotropic instability)と言う。 \(\partial\overline{u}/\partial y>0\)のところでは,\(\psi'\)が北西から南東に傾けば擾乱は発達する。 右辺第2項は,北向き温度フラックス\(\overline{v'T'}\)と基本東西風の鉛直シア(南北温度傾度 \(-\partial \overline{T}/\partial y\))との積に比例する擾乱のエネルギーが生ずることを示す。この過程を傾圧不安定(baroclinic instability)と言う。基本場から擾乱への傾圧エネルギー変換が正になるためには擾乱の軸は西に傾いていなければならない。
ところで,Equation 3.8より南北渦位フラックスは
\[\rho_0 \overline{v'q'} = \rho_0\frac{\partial}{\partial y}\overline{\frac{\partial \psi'}{\partial x}\frac{\partial\psi'}{\partial y}} + \frac{\partial}{\partial z^*}\left(\epsilon\rho_0\overline{\frac{\partial\psi'}{\partial x}\frac{\partial \psi'}{\partial z^*}}\right) \tag{3.11}\]
と書ける。
\[\left(\frac{\partial}{\partial t}+\overline{u}\frac{\partial}{\partial x}\right)\eta' = v'\]
で定義される南北変位\(\eta'\)を用いると
\[\begin{aligned}
q' &= -\eta'\frac{\partial\overline{q}}{\partial y}, \\
\overline{v'q'} &= -\frac{\partial\overline{q}}{\partial y}\frac{\partial}{\partial t}\frac{\overline{\eta^{'2}}}{2}
\end{aligned}\]
となる。上下端では,Equation 3.10 より
\[\overline{\frac{\partial\psi'}{\partial x}\frac{\partial\psi'}{\partial z^*}} = \frac{\partial\overline{u}}{\partial z^*}\frac{\partial}{\partial t}\frac{\overline{\eta^{'2}}}{2}\]
となる。 Equation 3.11 を子午面積分すると
\[\int\int\rho_0\frac{\partial\overline{q}}{\partial y}\frac{\partial}{\partial t}\overline{\eta^{'2}} \mathrm{d} y \mathrm{d} z^* - \int \left.\epsilon\rho_0 \frac{\partial\overline{u}}{\partial z^*}\frac{\partial}{\partial t}\overline{\eta^{'2}} \mathrm{d} y \right|_{z^*=0} = 0 \tag{3.12}\]
を得る。 ここで,上下端での摩擦がないとき
\[\frac{\partial}{\partial t}\int\int\rho_0\overline{u}\mathrm{d} y\mathrm{d} z^* = -\int\int \rho_0\frac{\partial}{\partial y}\overline{v'u'} \mathrm{d}y\mathrm{d} z^* = 0\]
であることを用い,\(z^*\rightarrow\infty\)で\(\eta' \rightarrow 0\)または\(\partial\overline{u}/\partial z \rightarrow 0\)として上端での南北温度フラックスの寄与を無視した。 擾乱が成長する(\(\partial \overline{\eta^{'2}}/\partial t>0\))とき,Equation 3.12 が成り立つためには,以下のいずれか満たさなければならない。
- \(z^* = 0\)で\(\partial \overline{u}/\partial z^* = 0\),即ち下端で南北温度傾度がないとき,\(\partial \overline{q}/\partial y\)は符号を変えなければならない(Rayleighの必要条件)。
- \(\partial \overline{q}/\partial y \ge 0\)がどこでも成り立つとき,下端のどこかで\(\partial \overline{u}/\partial z^* > 0\)でなければならない。
- \(\partial \overline{u}/\partial z^* < 0\)がどこでも成り立つとき,どこかで\(\partial \overline{q}/\partial y < 0\)でなければならない。
Equation 3.9 は
\[\frac{\partial\overline{q}}{\partial y} = \beta - \frac{\partial^2\overline{u}}{\partial y} - \epsilon\frac{\partial^2\overline{u}}{\partial z^{*2}} + \frac{\epsilon}{H}\frac{\partial\overline{u}}{\partial z^*} - \frac{\partial \epsilon}{\partial z^*}\frac{\partial\overline{u}}{\partial z^*}\]
と書ける。\(\beta>0\)なので\(\partial \overline{q}/\partial y < 0\)となるのは,曲率の大きなところである。ジェットは大きな南北シアを伴うことがあり,順圧不安定を起こすことがある。中緯度における傾圧不安定は,通常\(\partial \overline{q}/\partial y > 0\)で下端に西風シア\(\partial \overline{u}/\partial z^* > 0\)(南北温度傾度)を伴うところで生ずる。
Eady問題
Eady (1949) は以下のような仮定をおいて,線型安定性問題を解いた。
- 基本場の密度一定(Boussinesq近似)
- \(f\)平面(\(\beta=0\))
- 鉛直シア一定 (\(\overline{u}= \Lambda z^*\))
- \(z^* = 0\)と\(z^* = H\)は平坦な剛体底・天井 (rigid lid)。
この仮定の下では,擾乱の渦位方程式Equation 3.7は
\[\left(\frac{\partial}{\partial t}+\Lambda z^*\frac{\partial}{\partial x}\right)\left(\nabla^2\psi' + \epsilon\frac{\partial^2\psi'}{\partial z^{*2}}\right) = 0, \tag{3.13}\]
境界条件は
\[\left(\frac{\partial}{\partial t} + \Lambda z^*\frac{\partial}{\partial x}\right)\frac{\partial \psi'}{\partial z^*} - \Lambda\frac{\partial\psi'}{\partial x} = 0 \tag{3.14}\]
である。
ここで波動解
\[\psi' = \Re \Psi(z^*) \exp[i(kx+ly-kct)]\]
を仮定すると Equation 3.13 は
\[\left(\frac{\mathrm{d}^2}{\mathrm{d}z^{*2}}-\mu^2\right)\Psi = 0,\;\mu^2 \equiv \frac{k^2+l^2}{\epsilon} \tag{3.15}\]
Equation 3.14 は
\[(\Lambda z - c)\frac{\mathrm{d}\psi}{\mathrm{d}z^*} - \Lambda\Psi = 0,\; z^* = 0, H \tag{3.16}\]
となる。
Equation 3.16の一般解は
\[\Psi(z^*) = a\cosh\mu z^* + b \sinh\mu z^* \tag{3.17}\]
と書ける。これを\(z^*\)で微分すると
\[\frac{\mathrm{d}\Psi}{\mathrm{d}z^*} = a\mu\sinh\mu z^* + b\mu\cosh\mu z^* \tag{3.18}\]
となる。Equation 3.17,Equation 3.18を用いると,Equation 3.15は
\[\begin{aligned}
\begin{pmatrix}
\Lambda & c\mu \\
(\Lambda H - c)\mu\sinh(\mu H)-\Lambda\cosh(\mu H) & (\Lambda H - c)\mu\cosh(\mu H)-\Lambda\sinh(\mu H)
\end{pmatrix}
\begin{pmatrix}
a \\ b
\end{pmatrix} = 0
\end{aligned} \tag{3.19}\]
と書ける。非自明解は
\[c^2-\Lambda H c + \frac{\Lambda^2 H}{\mu}\coth(\mu H) - \frac{\Lambda^2}{\mu^2} = 0\]
の解で
\[c = \frac{\Lambda H}{2} \pm \frac{\Lambda}{\mu}\sqrt{\
\left(\frac{\mu H}{2} - \tanh\frac{\mu H}{2}\right)\
\left(\frac{\mu H}{2} - \coth\frac{\mu H}{2}\right)\
} \tag{3.20}\]
となる。Equation 3.20を求める際
\[\coth x = \dfrac{1}{2}\left(\tanh\frac{x}{2}+\coth\frac{x}{2}\right)\]
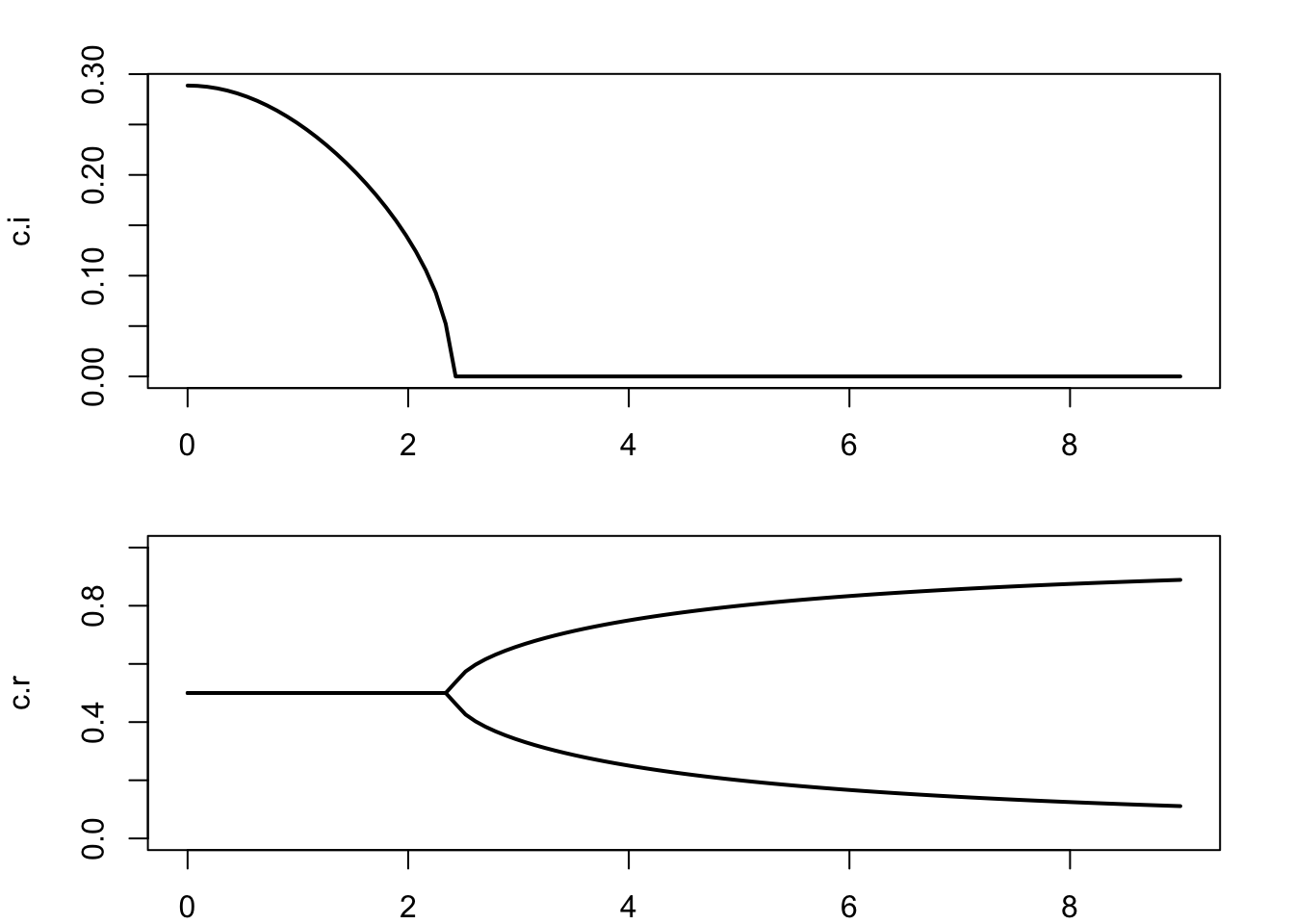
を用いた。 \(\mu H/2 \ge \tanh(\mu H/2)\)なので,\(\mu H/2 > \coth(\mu H/2)\)のとき,二つの解はともに実数である。 \(\mu H\)が大きくなると二つの解は,底と天井の風速に漸近する(Figure 3.1)。
Code
calc.c <- function(mu){
ifelse(mu == 0,
sqrt(-1/12 + 0i),
{
muh <- mu * 0.5
tanh.muh <- tanh(muh)
coth.muh <- 1 / tanh.muh
sqrt((muh - coth.muh) * (muh - tanh.muh) + 0i) / mu}
)
}
mu <- seq(0, 9, length.out = 101)
c.z <- calc.c(mu)
c.i <- Im(c.z)
c.r1 <- 0.5 + Re(c.z)
c.r2 <- 0.5 - Re(c.z)
par(mfrow = c(2, 1), mar = c(2, 4, 2, 2))
plot(mu, c.i, type = "l", lwd = 2, xlab = "μH")
plot(mu, c.r1, type = "l", lwd = 2, ylim = c(0, 1),
xlab = "μH", ylab = "c.r")
lines(mu, c.r2, lwd = 2)
虚部が現れる臨界値は\(\mu_\mathrm{c} H/2 = \coth(\mu_\mathrm{c} H/2)\)より
\[\mu_\mathrm{c}H \approx 2.3994 \tag{3.21}\]
で,\(\mu < \mu_\mathrm{c}\)のとき波は発達する(Figure 3.1)。
\(l=0\)のとき
\[\frac{\Lambda}{\mu} = \frac{\Lambda f_0}{kN^*}\]
なので,成長率は
\[kc_\mathrm{i} = \frac{\Lambda f_0}{N}\
\sqrt{\
\left(\frac{\mu H}{2} - \tanh\frac{\mu H}{2}\right)\
\left(\frac{\mu H}{2} - \coth\frac{\mu H}{2}\right)} \tag{3.22}\]
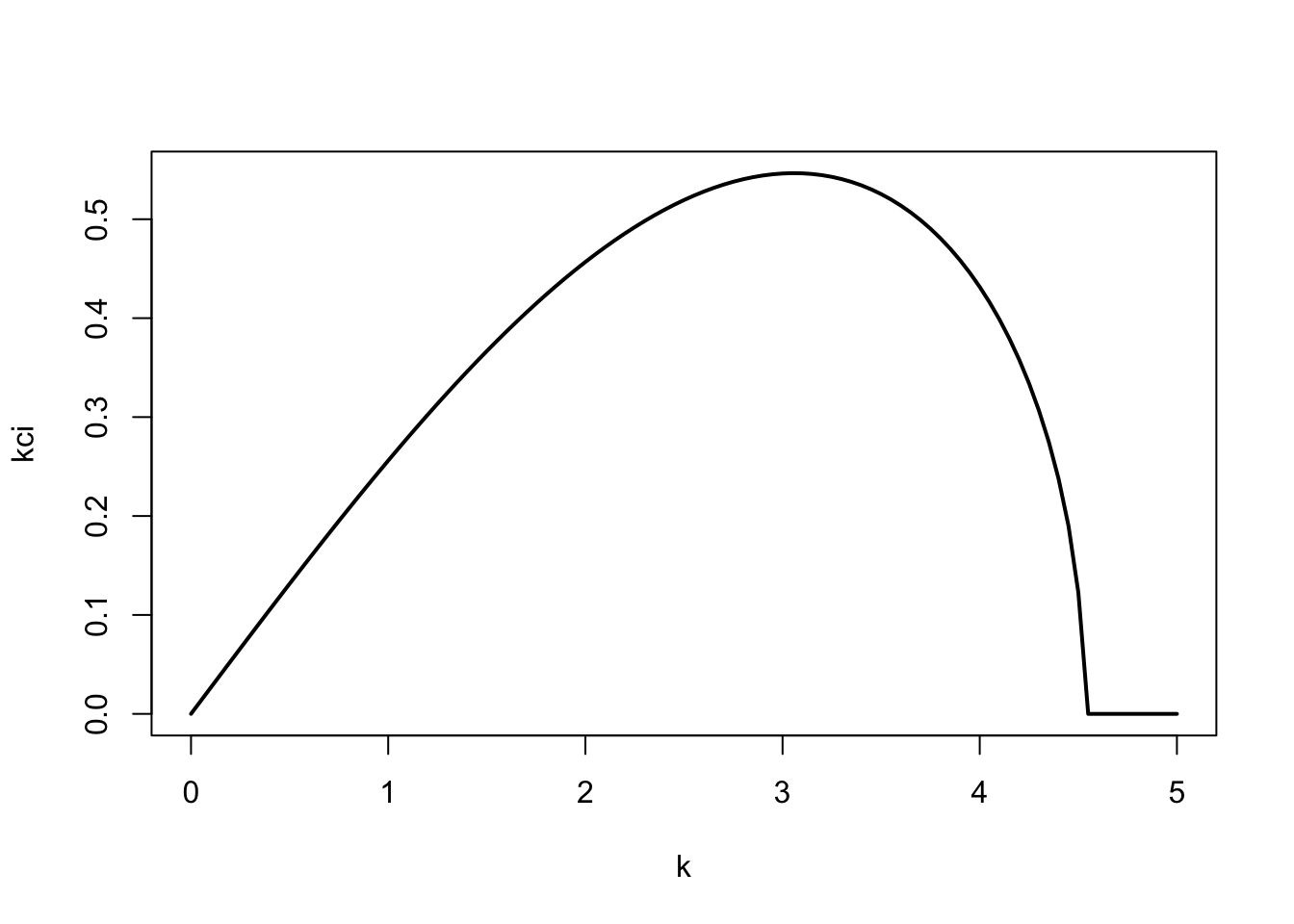
となる。 Equation 4.3 が最大になる波数は
\[\mu H = k_\mathrm{m}\frac{N^*H}{f_0} \approx 1.6061 \tag{3.23}\]
で,このときの成長率は
\[k_\mathrm{m}c_\mathrm{i}\frac{N^*}{\Lambda f_0} \approx 0.30982\]
Equation 3.23は,Rossbyの変形半径を\(NH/f \approx 10^6\)とすると,約4000 kmとなる。成長率は,およそ1 day\(^{-1}\)である(Figure 3.2)。
Code
calc.mu <- function(k, n = 0, S = 0.25) {
sqrt((k^2 + ((n + 0.5) * pi)^2) * S)
}
k <- seq(0, 5, length.out = 101)
kci <- k * Im(calc.c(calc.mu(k)))
plot(k, kci, type = "l", lwd = 2)
Equation 3.19 より\(b=-\Lambda a/\mu c\)なので
\[\begin{aligned}
\Psi(z^*) &= \cosh(\mu z^*) - \frac{\Lambda}{\mu c}\sinh(\mu z^*) \\
&= \left(\cosh(\mu z^*) - \frac{\Lambda c_\mathrm{r}}{\mu |c|^2}\sinh(\mu z^*)\right) +
i\frac{\Lambda c_\mathrm{i}}{\mu |c|^2}\sinh(\mu z^*)
\end{aligned}\]
となる。ここで
\[\dfrac{1}{c} = \frac{1}{c_\mathrm{r}+ic_\mathrm{i}} = \frac{c_\mathrm{r}-ic_\mathrm{i}}{|c|^2}\]
を用いた。線型論では,擾乱の振幅は求まらないことに注意する。\(\psi'\)は
\[\begin{aligned}
\psi' &= \Re \exp(kc_\mathrm{i}t)\cos(ly)\Psi(z^*)\exp[ik(x-c_\mathrm{r}t)] \\
& = \exp(kc_\mathrm{i}t))|\Psi(z^*)|\cos(ly)\cos[kx + \alpha(z^*) - kc_\mathrm{r}t]
\end{aligned} \tag{3.24}\]
と書ける。ここで
\[|\Psi(z)|^2 = \left(\cosh(\mu z^*) - \frac{\Lambda c_\mathrm{r}}{\mu |c|^2}\sinh(\mu z^*)\right)^2 + \frac{\Lambda^2 c_\mathrm{i}^2}{\mu^2 |c|^4}\sinh^2(\mu z^*) \tag{3.25}\]
\[\tan\alpha(z^*) = \frac{\Lambda c_\mathrm{i}}{\mu|c|^2\coth(\mu z^*) - \Lambda c_\mathrm{r}} \tag{3.26}\]
である。
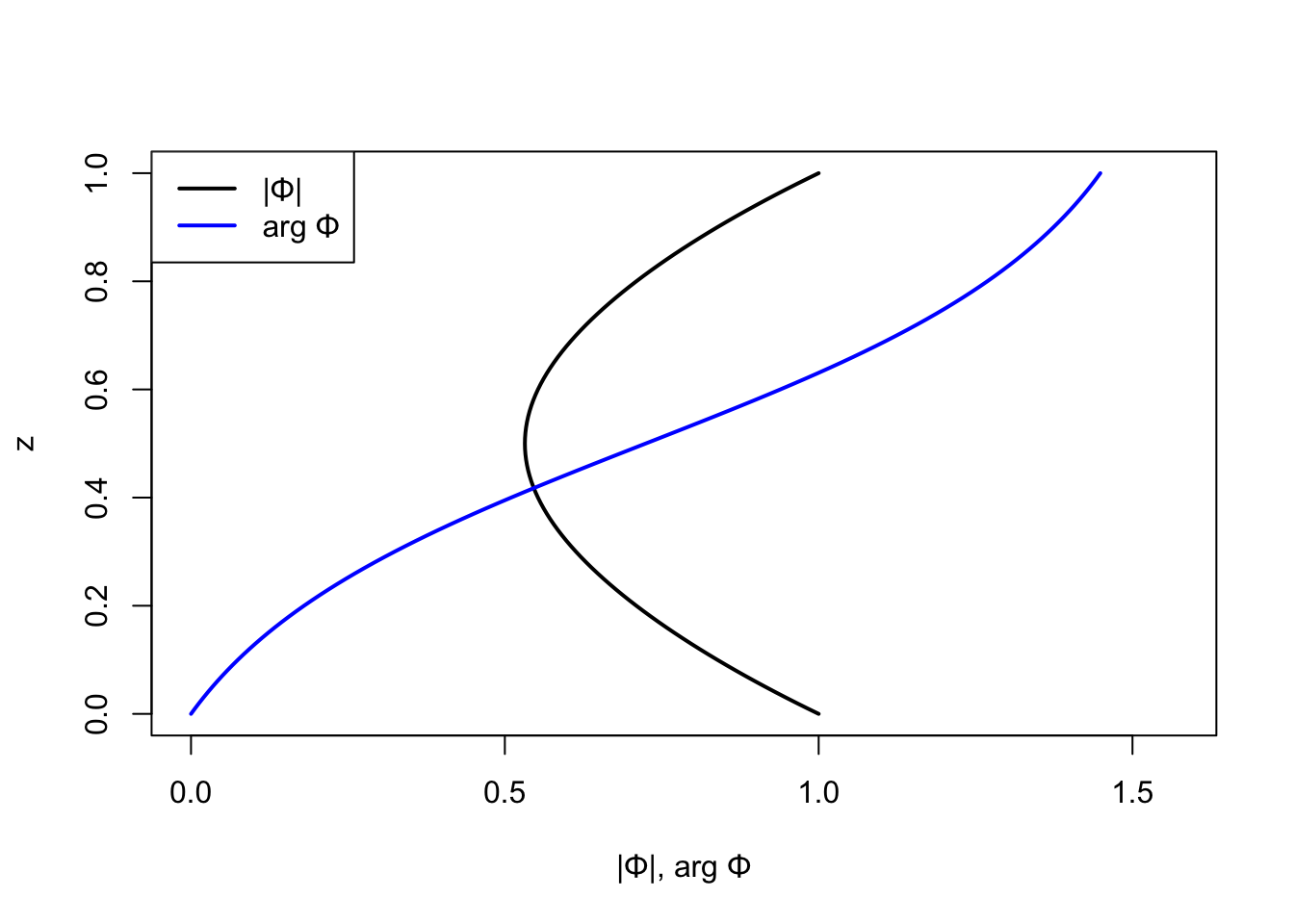
\[x = -\frac{\alpha(z^*)}{k} + \mathrm{const}\]
となるので,等位相線は西に傾くことが分る(Figure 3.3)。
Code
k <- 3.1277
mu <- calc.mu(k)
z <- seq(0, 1, length.out = 101)
muz <- mu * z
c.z <- calc.c(mu)
c.r <- 0.5
c.i <- Im(c.z)
muc.2 <- mu * (c.r^2 + c.i^2)
x <- cosh(muz) - 0.5 * sinh(muz) / muc.2
y <- c.i * sinh(muz) / muc.2
phi <- sqrt(x^2 + y^2)
alpha <- atan2(y, x)
plot(phi, z, type = "l", xlim = c(0, pi / 2), lwd = 2, xlab = "|Φ|, arg Φ")
lines(alpha, z, lwd = 2, col = "blue")
legend("topleft", c("|Φ|", "arg Φ"), lwd = 2, col = c("black", "blue"))
Equation 3.24を\(x, y, z\)で微分し,運動量及び熱フラックスを計算する。\(u'\)と\(v'\)は90\(^\circ\)位相がずれているので,
\[\rho_0\overline{\frac{\partial\psi'}{\partial x}\frac{\partial\psi'}{\partial y}} = 0 \tag{3.27}\]
である。熱フラックスは
\[\rho_0 \overline{\frac{\partial\psi'}{\partial x}\frac{\partial\psi'}{\partial z^*}} = \rho_0\exp(2kc_\mathrm{i}t)\frac{|\Psi(z^*)|^2}{2}k\frac{\partial\alpha(z^*)}{\partial z^*}\cos^2(ly) \tag{3.28}\]
と書ける。\(\partial\alpha/\partial z^*\)は正なので,熱フラックスは北向きで,基本場の温度傾度と逆方向である。 Equation 3.25 とEquation 3.26を用いると,熱フラックスは高さに依存しないことを示すことができる。 Eady問題では\(\partial\overline{q}/\partial y=0\)なので,渦位フラックス
\[\overline{v'q'} = 0\]
である。
Eady, E. T., 1949: Long waves and cyclone waves.
Tellus,
1, 33–52,
https://doi.org/10.1111/j.2153-3490.1949.tb01265.x.
Pedlosky, J., 1987: Geophysical fluid dynamics. Second. Springer-Verlag,.