2 準地衡方程式系と鉛直循環
この講義では,準地衡風方程式系における鉛直循環について学ぶ。簡潔に表記される気圧に基づく鉛直座標を用いる。
2.1 気圧座標
一般化された鉛直座標(Appendix B)で\(s = p\)とすると,\(p\)座標における支配方程式系は次のように書ける。
運動方程式
\[\frac{\mathrm{d}\pmb{v}}{\mathrm{d}t} + f\pmb{k}\times\pmb{v} = -g\nabla z\]
ここで
\[\frac{\mathrm{d}}{\mathrm{d}t} = \frac{\partial}{\partial t} + \pmb{v}\cdot\nabla + \omega\frac{\partial}{\partial p},\;\omega \equiv \frac{\mathrm{d}p}{\mathrm{d}t} \tag{2.1}\]
静力学平衡
\[g\frac{\partial z}{\partial p} = -\alpha,\; \alpha\equiv \dfrac{1}{\rho}\]
連続の式
\[\nabla\cdot\pmb{v}+\frac{\partial\omega}{\partial p}=0\]
熱力学の式
\[\frac{\mathrm{d}\ln\theta}{\mathrm{d}t} = \frac{\dot{Q}}{c_pT} \tag{2.2}\]
2.2 準地衡風方程式系
\(\beta\)平面近似
\[f = f_0+\beta y,\;\beta\equiv\frac{\mathrm{d}f}{\mathrm{d}y}\]
地衡風
\[\begin{aligned} u_\mathrm{g} &= -\dfrac{1}{f_0}\frac{\partial\phi}{\partial y} \\ v_\mathrm{g} &= \dfrac{1}{f_0}\frac{\partial\phi}{\partial x} \end{aligned} \tag{2.3}\]
ラグランジュ微分とオイラー微分との関係
\[\frac{\mathrm{d}_\mathrm{g}}{\mathrm{d}t} = \frac{\partial}{\partial t} + u_\mathrm{g}\frac{\partial}{\partial x} + v_\mathrm{g}\frac{\partial}{\partial y}\]
運動方程式
\[\frac{\mathrm{d}_\mathrm{g}u_\mathrm{g}}{\mathrm{d}t} = f_0v_\mathrm{a} +\beta yv_\mathrm{g} \tag{2.4}\]
\[\frac{\mathrm{d}_\mathrm{g}v_\mathrm{g}}{\mathrm{d}t} =-f_0u_\mathrm{a} -\beta yu_\mathrm{g} \tag{2.5}\]
Equation 2.5を\(x\)で微分したものから,Equation 2.4を\(y\)で微分したものを引くと,渦度方程式
\[\frac{\mathrm{d}_\mathrm{g}\zeta_\mathrm{g}}{\mathrm{d}t} + \beta v_\mathrm{g} = \frac{\mathrm{d}_\mathrm{g}}{\mathrm{d}t}(f + \zeta_\mathrm{g}) = f_0\frac{\partial\omega}{\partial p}\]
が得られる。ここで準地衡渦度\(\zeta_\mathrm{g}\)は
\[\zeta_\mathrm{g} \equiv \frac{\partial v_\mathrm{g}}{\partial x}-\frac{\partial u_\mathrm{g}}{\partial y} = \frac{1}{f_0}\nabla^2\phi \tag{2.6}\]
と定義される。
静力学平衡
\[\frac{\partial \phi}{\partial p} = -\alpha \tag{2.7}\]
連続の式
\[\nabla \cdot \pmb{v}_\mathrm{g} = 0 \tag{2.8}\]
\[\nabla \cdot \pmb{v}_\mathrm{a}+\frac{\partial \omega}{p} = 0 \tag{2.9}\]
熱力学の式
\[\frac{\mathrm{d}_\mathrm{g}\theta}{\mathrm{d}t}+\omega\frac{\mathrm{d}\theta_0}{\mathrm{d}p}=\frac{\theta_0}{c_pT_0}\dot{Q}\]
ここで\(\theta\)は,基本場\(\theta_0(p)\)からのずれで,偏差を示す\('\)は省略する。
\[\theta_{\mathrm{total}}(x, y, p, t) = \theta_0(p) + \theta(x, y, p, t)\]
熱力学の式は気温\(T\)を使って
\[\frac{\mathrm{d}_\mathrm{g}T}{\mathrm{d}t} -\frac{p}{R}S_0\omega = \frac{\dot{Q}}{c_p} \tag{2.10}\]
と表すこともできる。ここで
\[S_0\equiv-\frac{\alpha_0}{\theta_0}\frac{\mathrm{d}\theta_0}{\mathrm{d}p}\]
は,基本場の安定度を示す。 また,Equation 2.7を用いると
\[\frac{\mathrm{d}_\mathrm{g}}{\mathrm{d}t} \left(\frac{\partial\phi}{\partial p}\right) + S_0\omega = -\frac{R\dot{Q}}{c_p p} \tag{2.11}\]
と書ける。
2.3 \(\omega\)方程式
準地衡風方程式系における鉛直循環を診断する古典的な\(\omega\)方程式を導出する。 簡単のため,\(f\)平面(\(f=f_0\))上で断熱(非断熱加熱\(\dot{Q}=0\))の場合を考える。 渦度方程式Equation 2.6を\(f_0\)倍して\(p\)で微分したものから,熱力学方程式Equation 2.11に\(\nabla^2\)を作用させたものを引くと
\[\left(S_0\nabla^2 + f_0^2\frac{\partial^2}{\partial p^2}\right)\omega = F_1 + F_2\]
を得る。ここで
\[\begin{aligned} F_1 &= f_0\frac{\partial }{\partial p}\left(u_\mathrm{g}\frac{\partial }{\partial x} + v_\mathrm{g}\frac{\partial }{\partial y}\right)\left(f + \zeta_\mathrm{g}\right) \\ F_2 &= \nabla^2\left(u_\mathrm{g}\frac{\partial }{\partial x} + v_\mathrm{g}\frac{\partial }{\partial y}\right)\left(-\frac{\partial \phi}{\partial p}\right) \end{aligned}\]
である。\(F_1\)は絶対渦度の移流の高度変化を表し,差分渦度移流(differential vorticity advection)と呼ばれる。 \(F_2\)は,温度移流の\(\nabla^2\)に比例する。両者には異符号の共通項があり相殺するため,必ずしも適切な解釈ができるとは限らない。
2.4 Qベクトル
以下のように温度風平衡から導出すると,鉛直流\(\omega\)を駆動する強制項を簡潔に表現することができ,古典的な\(\omega\)方程式に比べて明瞭な解釈が可能である。
2.4.1 Qベクトルの導出
\(f\)平面(\(f=f_0\))上で断熱(非断熱加熱\(\dot{Q}=0\))のとき運動方程式Equation 2.4,Equation 2.5は
\[\frac{\mathrm{d}_\mathrm{g}u_\mathrm{g}}{\mathrm{d}t}=f_0v_\mathrm{a},\; \frac{\mathrm{d}_\mathrm{g}v_\mathrm{g}}{\mathrm{d}t} = -f_0u_\mathrm{a}\]
となる。 Equation 2.3の右辺を\(p\)で微分し,静力学平衡Equation 2.7を用いると温度風平衡
\[f_0\frac{\partial u_\mathrm{g}}{\partial p} =\frac{R}{p}\frac{\partial T}{\partial y} \tag{2.12}\]
\[f_0\frac{\partial v_\mathrm{g}}{\partial p} =-\frac{R}{p}\frac{\partial T}{\partial x} \tag{2.13}\]
が得られる。 Equation 2.12の右辺のラグランジュ微分(\(\mathrm{d}_g/\mathrm{d}t\))をとると
\[\frac{\mathrm{d}_\mathrm{g}}{\mathrm{d}t}\left(\frac{R}{p}\frac{\partial T}{\partial y}\right) = S_0\frac{\partial\omega}{\partial y}+Q_y \tag{2.14}\]
となる。ここで,
\[Q_y \equiv -\frac{R}{p}\frac{\partial\pmb{v}_\mathrm{g}}{\partial y}\cdot\nabla T \tag{2.15}\]
である。 Equation 2.12の左辺をラグランジュ微分し,Equation 2.12,Equation 2.13を用いると
\[\frac{\mathrm{d}_\mathrm{g}}{\mathrm{d}t}\left(f_0\frac{\partial u_\mathrm{g}}{\partial p}\right) = f_0^2\frac{\partial v_\mathrm{a}}{\partial p}-Q_y \tag{2.16}\]
となる。 Equation 2.14,Equation 2.16より,
\[S_0\frac{\partial \omega}{\partial y}-f_0^2\frac{\partial v_\mathrm{a}}{\partial p} = -2Q_y \tag{2.17}\]
が得られる。 同様にEquation 2.12のラグランジュ微分から,
\[S_0\frac{\partial \omega}{\partial x}-f_0^2\frac{\partial u_\mathrm{a}}{\partial p} = -2Q_x \tag{2.18}\]
\[Q_x \equiv -\frac{R}{p}\frac{\partial \pmb{v}_\mathrm{g}}{\partial x}\cdot\nabla T \tag{2.19}\]
を得る。 Equation 2.17を\(y\),Equation 2.18を\(x\)で微分して加え, 連続の式Equation 2.9を用いると \(\omega\) に関する診断の式
\[\left(S_0\nabla^2+f_0^2\frac{\partial^2}{\partial p^2}\right)\omega = -2\nabla\cdot\pmb{Q} \tag{2.20}\]
を得る。ここで\(\pmb{Q}\equiv(Q_x, Q_y)\)はQベクトルと呼ばれる(Hoskins et al. 1978) 。
2.4.2 非地衡風成分の役割
準地衡風方程式系における非地衡風成分の役割について考えよう。非地衡風成分がないとき,Equation 2.14は地衡風成分のみで強制された気温傾度の時間変化
\[\frac{\mathrm{d}_\mathrm{g}}{\mathrm{d}t}\left(\frac{R}{p}\frac{\partial T}{\partial y}\right) = Q_y\]
Equation 2.16は鉛直シアの変化
\[\frac{\mathrm{d}_\mathrm{g}}{\mathrm{d}t}\left(f_0\frac{\partial u_\mathrm{g}}{\partial p}\right) = -Q_y\]
を表す。これらは大きさが同じで符号が反対なので,温度風平衡を壊すように働いている。つまり,温度風平衡は非地衡風成分による鉛直循環により維持されている。
2.4.3 Qベクトルの見方
高度場や気温の分布が与えられたときに,Qベクトルがどのようになるか理解するため,簡単な場合について考えてみよう(Sanders and Hoskins 1990) 。 Equation 2.15及びEquation 2.19で等温線と平行に\(x\)軸をとると\(\partial T/\partial x = 0\)となるので
\[\pmb{Q} = -\frac{R}{p}\frac{\partial T}{\partial y}\left(\frac{\partial v_\mathrm{g}}{\partial x},-\frac{\partial u_\mathrm{g}}{\partial x}\right) = -\frac{R}{p}\left|\frac{\partial T}{\partial y}\right|\left(\pmb{k}\times\frac{\partial \pmb{v}_\mathrm{g}}{\partial x}\right) \tag{2.21}\]
と変形することができる。すなわち,\(\pmb{Q}\)は左手が寒気となるようにとった\(x\)軸方向に沿う地衡風ベクトルの変化(\(\partial \pmb{v}_\mathrm{g}/\partial x\))を90° 時計回りに回転(\(-\pmb{k}\times\)したものに比例(\(R/p\vqty{\partial T/\partial y}\))する。
Qベクトルの性質をまとめると以下の通りである。
- Qベクトルは,収束域で上昇流,発散域で下降流を強制するEquation 2.20。
- Qベクトルは,北風から南風に変わる低気圧の中心では東向き(温度風の向き),南から北風に変わる高気圧の中心では西向き(温度風と反対向き)となり,低気圧の前面で上昇流,後面で下降流を強制する。
- 等温線と等高線が平行で温度移流のない場合でも,風向きが北西から南西に変わる谷(トラフ)でQベクトルは東向きとなり,低気圧の前面に上昇流を強制する。
- 北風と南風とが合流する前線形成場では,東ほど風が強くなるため,Qベクトルは南向きとなり,前線の南の温暖域で上昇流を強制する。
- 暖気に向いたQベクトルは前線形成,等温線と平行なQベクトルは不活発,寒気に向いたQベクトルは前線消滅を示す。
連続の式を用いずにEquation 2.21を
\[\pmb{Q} = -\frac{R}{p}\frac{\partial T}{\partial y}\left(\frac{\partial v_\mathrm{g}}{\partial x},\frac{\partial v_\mathrm{g}}{\partial y}\right) \tag{2.22}\]
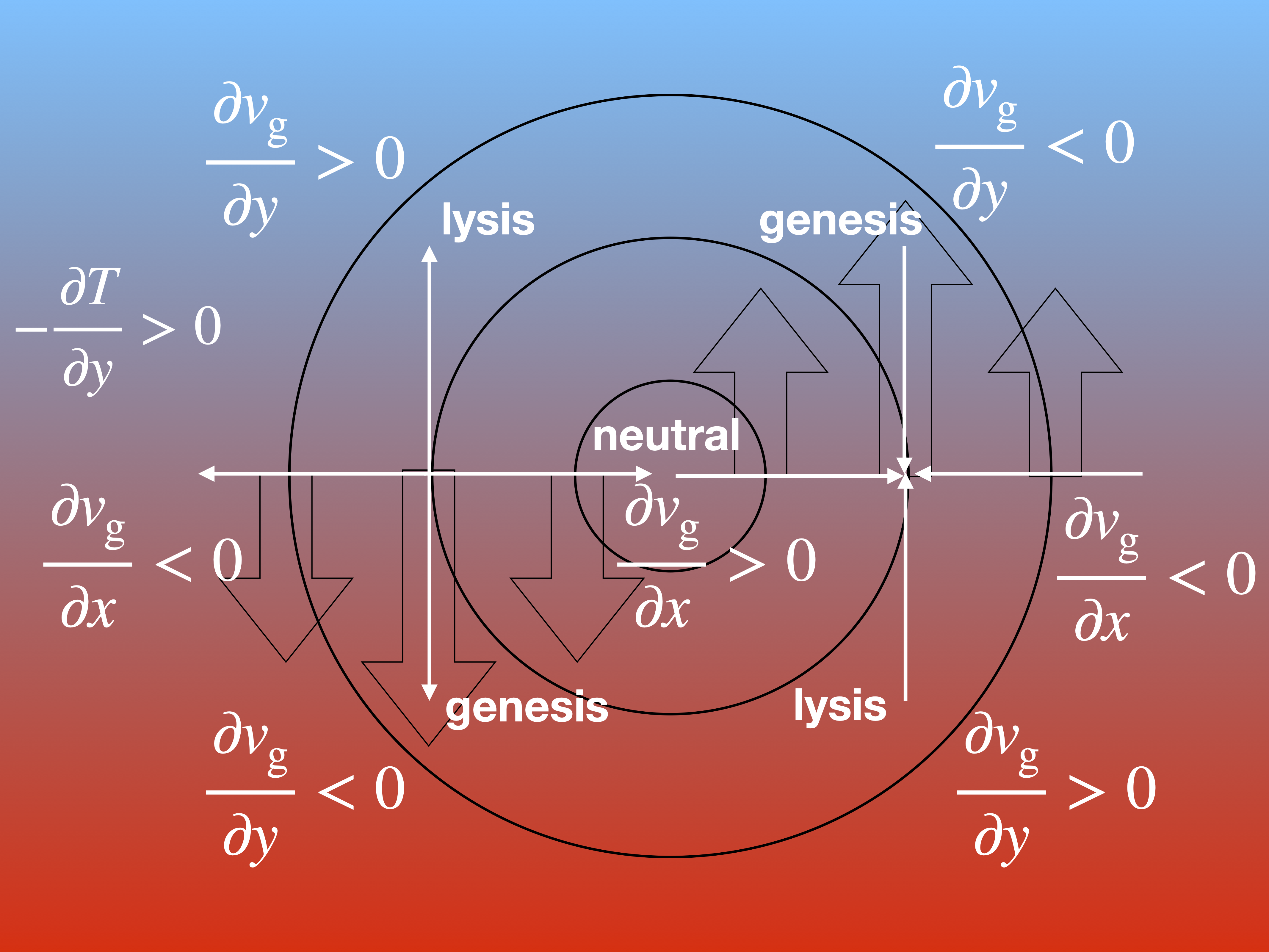
と表すと,\(v_\mathrm{g}\)のシアーのみでQベクトルが決まる(Equation 2.22)。 \(\partial v_\mathrm{g}/\partial x\)は北風最大の西で負,東で正,\(\partial v_\mathrm{g}/\partial y\)は北風最大の北で正,南でなので,北風最大の周りでQベクトルは発散する。
2.5 実際の例
NCEP/NCAR再解析(Kalnay et al. 1996)を用いて行なったQベクトル解析の例を示す。
2.5.1 北米東岸の低気圧
1975年11月10日0 UTC,北米東岸の低気圧(Hoskins and Pedder 1980)の例では,700 hPa面の谷の後面(西側)に寒気がある) 。 これに対応して,下降流とこれに対応するQベクトルの発散が見られる。 低気圧の前面では,Qベクトルが収束している。これよりも弱いが,寒冷前線でもQベクトルが見られる。等温線を横切っているので,前線形成が示唆される。一方,温暖前線ではQベクトルは等温線に平行であり重要でないことが分る。
2.5.2 西日本豪雨
2018年6月下旬から7月上旬にかけて,台風や梅雨前線の影響により,西日本の広い範囲で記録的な降水量を観測し, 各地で水害や土砂災害を引き起こした。 気象庁が「平成30年7月豪雨」と命名したこの現象は「西日本豪雨」として知られている。 降水量のピークは7月6日であったが,これに先行する7月4日に台風第7号が日本海を北東進し温低化している。 北風の極大からQベクトルが発散し,大陸から西日本に伸びる暖域に向かって収束している。 したがって,台風は梅雨前線の強化に寄与したと考えられる(Enomoto 2019) 。
- Equation 2.4,Equation 2.5から絶対渦度方程式Equation 2.6を導出せよ。
- Equation 2.7を用いてEquation 2.10を\(\partial \phi/\partial p\)で表し、Equation 2.11を導出せよ。
- 絶対渦度方程式と\(\partial \phi/\partial p\)で表した熱力学の式から時間微分の項を消去して,\(\omega\)方程式を導き,Equation 2.20と比較せよ。
- 低気圧の事例を選んでQベクトルを描け。領域はどこでもよい。高度を変えるとどうなるか。 参考: Pythonによる気象データサイエンス 梅雨前線