主成分分析は，回帰とともによく用いられる統計手法です。主成分分析は，ビッグデータを要約することができます。気象学では経験的直交函数（Empirical Orthogonal Functions, EOF），機械学習では次元削減手法として用いられる特異値分解，様々な分野の数値解析に用いられる固有値解析としても知られています。Rを使って手を動かしながらどのような手法か学んでいきましょう。
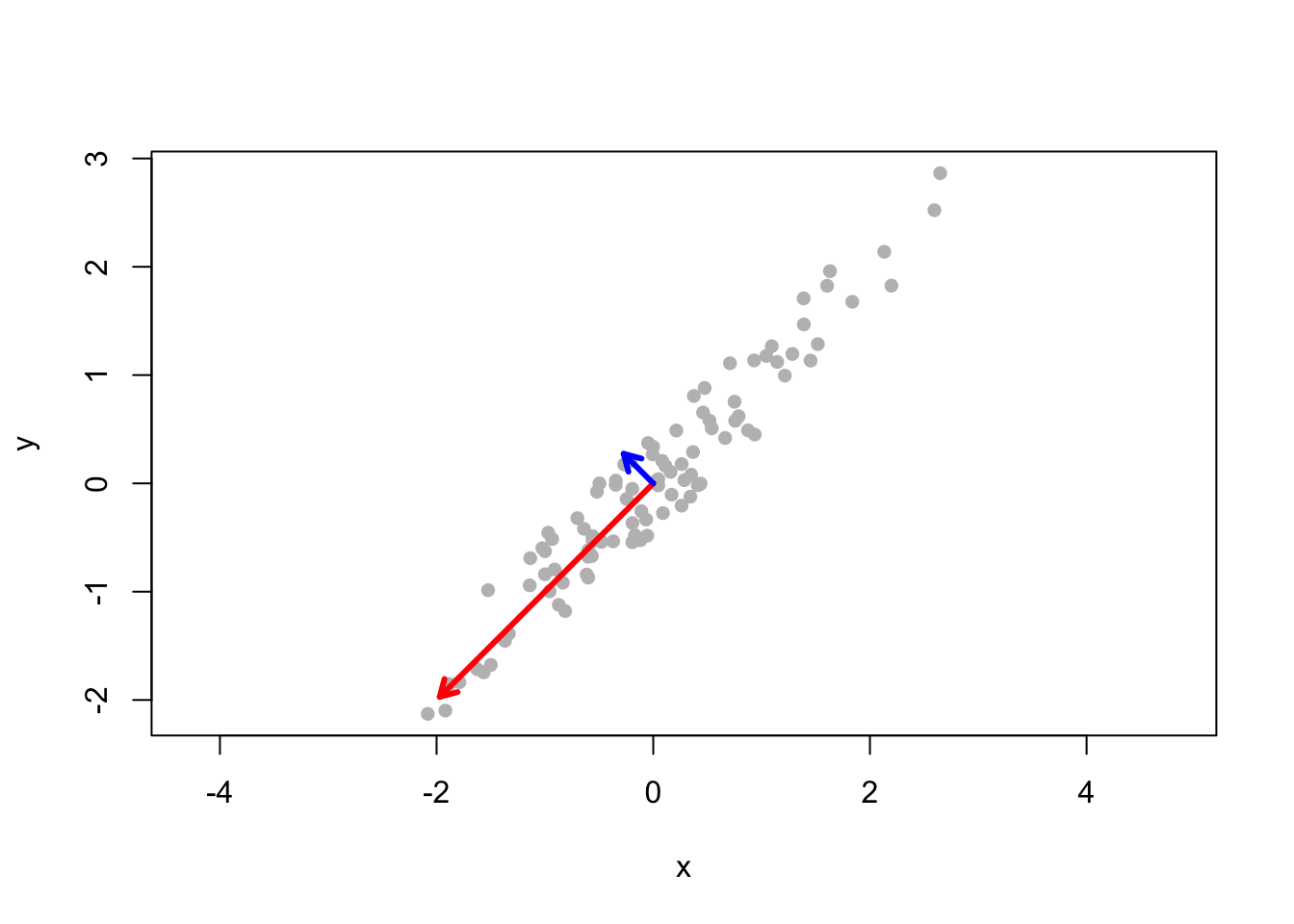
100個の観測が2組得られたとします。二つの組には何らかの関係があります。ばらつきの大きい方向を特異値解析で求めましょう。
m <- 100
set.seed(514)
x <- rnorm(m)
x <- (x - mean(x)) / sd(x)
y <- x + runif(m)
y <- (y - mean(y)) / sd(y)
amat <- cbind(x, y)
usv <- svd(amat)
v1 <- usv$d[1] * usv$v[, 1] * 0.2
v2 <- usv$d[2] * usv$v[, 2] * 0.2
plot(x, y, col="gray", pch=16, asp=1)
arrows(0, 0, v1[1], v1[2], length=0.1, lwd=3, col="red")
arrows(0, 0, v2[1], v2[2], length=0.1, lwd=3, col="blue")
乱数でxを生成し，それを少し乱したyを作ります。標準化した後100×2の配列amatにまとめます。これをsvd()で特異値分解をしてばらつきの大きい方向（固有ベクトル）を求めています。●はデータ，→は右特異ベクトルで特異値に比例させています。赤，青はそれぞれ1番目，2番目に分散が大きい方向を表します。
カラーパレットはpalette()にパレット名を渡すと確認できます。 引数なしだとRGBのHEX値が表示されます。 パレットの名前はpalette.pals()で確認できます。
palette.pals() [1] "R3" "R4" "ggplot2" "Okabe-Ito"
[5] "Accent" "Dark 2" "Paired" "Pastel 1"
[9] "Pastel 2" "Set 1" "Set 2" "Set 3"
[13] "Tableau 10" "Classic Tableau" "Polychrome 36" "Alphabet" 既定のカレーパレットはR4です。
k <- length(palette("R4"))
par(mar=rep(0, 4)); plot.new(); plot.window(c(0, k+1), c(0, 0.15))
points(1:k, rep(0.1, k), col=1:k, pch=15, cex=2)
text(1:k, 0.1, pos=rep(c(1, 3), length.out=k), palette(), col=1:k)
matplotlibで採用されている、tableau風の配色はTableau10です。
k <- length(palette("Tableau10"))
par(mar=rep(0, 4)); plot.new(); plot.window(c(0, k+1), c(0, 0.15))
points(1:k, rep(0.1, k), col=1:k, pch=15, cex=2)
text(1:k, 0.1, pos=rep(c(1, 3), length.out=k), palette(), col=1:k)
ここで，特異値解析と固有値解析との関係についておさらいをしておきます。ここではデータは実数とします。特異値分解は，\(m\)個のデータ\(n\)組を並べた\(m\times n\)行列\(\mathbf{X}\)を
\[ \mathbf{X} = \mathbf{USV}^T \tag{5.1}\]
のように分解するものです。\(\mathbf{U}\)は\(m\times m\)行列，\(\mathbf{S}\)は\(m\times n\)行列，\(\mathbf{V}\)は\(n\times n\)行列です。\(\mathbf{U}\)は左特異ベクトル，\(\mathbf{V}\)は右特異ベクトルと呼ばれています。特異値は\(\mathbf{S}\)の対角成分として最大\(m\)と\(n\)の小さい方の個数（\(p = \min(m, n)\)）が得られます。\(\mathbf{U}\)と\(\mathbf{V}\)はともに直交行列で\(\mathbf{U}^T\mathbf{U}=\mathbf{UU}^T=\mathbf{I}\)，\(\mathbf{V}^T\mathbf{V}=\mathbf{VV}^T=\mathbf{I}\)が成り立ちます。
print(usv$d)[1] 13.937893 1.932649print(usv$v) [,1] [,2]
[1,] -0.7071068 -0.7071068
[2,] -0.7071068 0.7071068wv <- eigen(t(amat) %*% amat)
print(sqrt(wv$values))[1] 13.937893 1.932649print(wv$vectors) [,1] [,2]
[1,] 0.7071068 -0.7071068
[2,] 0.7071068 0.7071068