4  回帰分析

4.1 統計

Rでは統計量を簡単に計算できます。 ベクトルに対する函数をいくつか挙げます。

統計量	Rの函数	統計量	Rの函数
平均	mean()	中央値	median()
最大値	max()	最小値	min()
範囲	range()	累積和	cumsum()
和	sum()	積	prod()
逆順	rev()	整列化	sort()
順位	rank()	元位置	order()

• sort()は小さい順に整列化します。
• rank()は整列化前の元の並びでの整列化の順位を返します。
• order()は整列化後に各要素が整列化前にいた位置を返します。

4.2 線型回帰

回帰分析（regression analysis）は、二つの変数の\(x\)と\(y\)のデータが与えられたときに、\(y=f(x)\)というモデルを当てはめます。 \(x\)を説明変数、\(y\)を目的変数と呼び、\(x\)がスカラーの場合を単回帰（simple regression）、ベクトルの場合を重回帰（multiple regression）と言います。 モデルが線型\(f(x) = \beta_0 + \beta_1 x\)なら、線型回帰、\(f(x)=ax^b, f(x)=ae^{bx}, f(x)=a + b\log x\)のように非線型なら非線型回帰といいます。 様々な当てはめ（curve-fitting）があります。

\(n\)個の観測\(y_1, \dots, y_n\)が与えられたとき、線型モデルでは次のように書けます。

\[ y_i = \beta_0 + \beta_1 x_i + \varepsilon_i \tag{4.1}\]

\(\varepsilon_i\)は誤差を表しています。 最小分散推定（minimum variance）は最小二乗法（method of least squares）とも呼ばれ、誤差の分散

\[S=\sum_i \varepsilon_i^2 \tag{4.2}\] を最小にする\(\beta_0,\,\beta_1\)を求めます。

Equation 4.2を\(\beta_0,\,\beta_1\)で微分して0と置くと、正規方程式

\[ \begin{aligned} \frac{\partial S}{\partial \beta_0} &= -2\sum[y_i - (\beta_0 + \beta_1 x_i)] = 0\\ \frac{\partial S}{\partial \beta_1} &= -2\sum[y_i - (\beta_0 + \beta_1 x_i)]x_i = 0 \end{aligned} \tag{4.3}\]

平均

\[ \bar{x} = \frac{1}{n}\sum{x_i},\;\bar{y} = \frac{1}{n}\sum{y_i} \] を用いると、Equation 4.3 の最初の式から

\[ \bar{y} = \beta_0 + \beta_1\bar{x} \tag{4.4}\]

が得られます。 \[ \begin{aligned} \sum (x_i-\bar{x})\bar{x} &= \bar{x}\sum{x_i} - n\bar{x}^2 = 0\\ \sum (y_i-\bar{y})\bar{x} &= \bar{x}\sum{y_i} - n\bar{x}\bar{y} = 0 \end{aligned} \] を用いると \[ \begin{aligned} \hat{\beta}_0 &= \bar{y} - \beta_1\bar{x}\\ \hat{\beta}_1 & = \frac{\sum(x_i-\bar{x})(y_i-\bar{y})}{\sum(x_i-\bar{x})^2} = \frac{\mathrm{cov}(x,\,y)}{\mathrm{var}(x)} \end{aligned} \] を得ます。 \(\hat{\beta}_1\)を回帰係数といいます。

df <- read.csv("co2_annual_20221026.csv")
beta1 <- cov(df$year, df$co2.global.mean.ppm.) / var(df$year)
beta0 <- mean(df$co2.global.mean.ppm.) - beta1 * mean(df$year)
print(c(beta0, beta1))

[1] -3427.371014     1.899497

実はRには回帰分析をする函数lm()があります。

lm.co2 <- lm(df$co2.global.mean.ppm. ~ df$year)
print(lm.co2$coefficients)

 (Intercept)      df$year 
-3427.371014     1.899497 

グラフに回帰直線を入れてみましょう。

plot(df$year, df$co2.global.mean.ppm.,
     main="Global Mean CO2 concentration",
     xlab="year", ylab="CO2 ppm")
abline(lm.co2)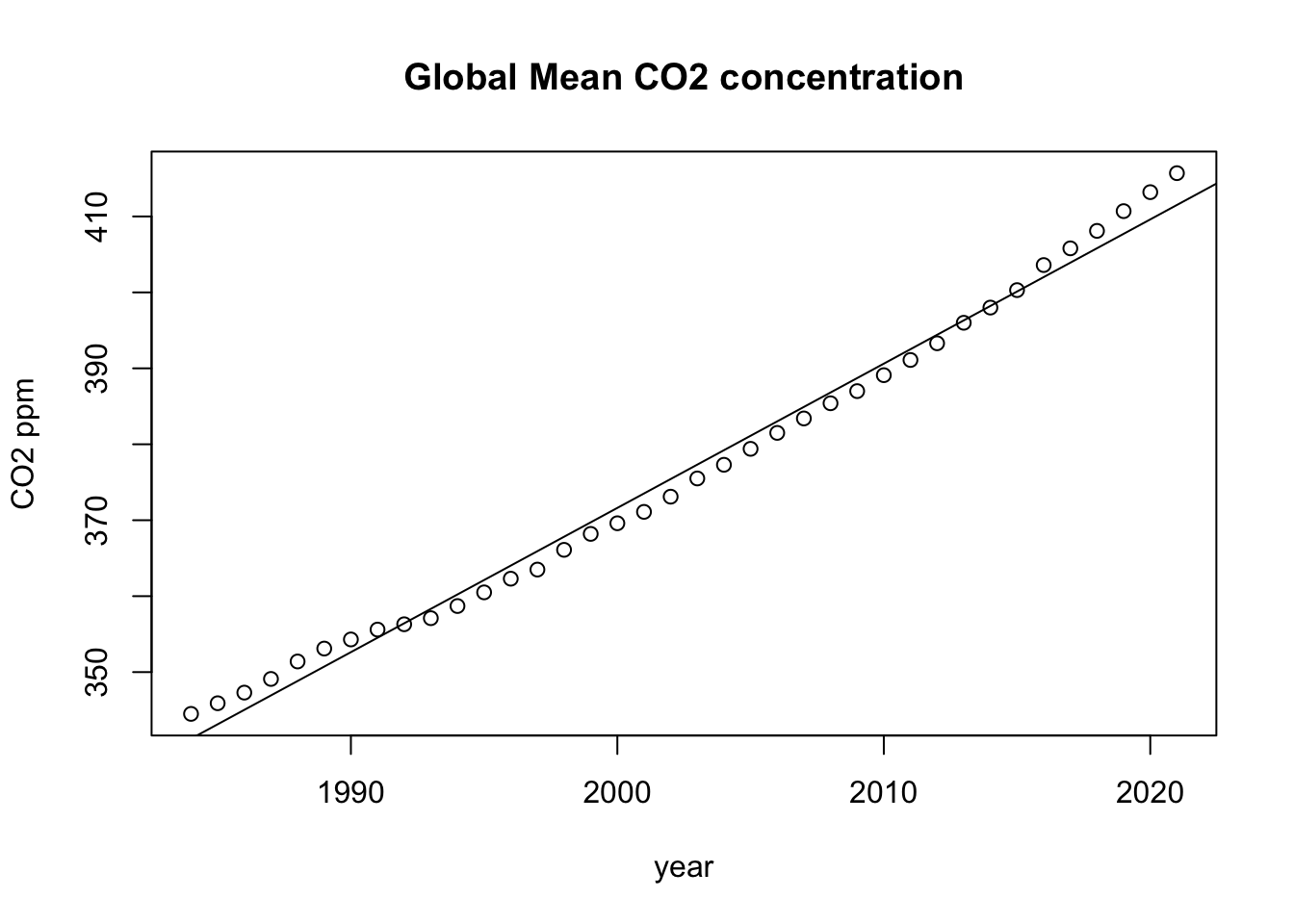

4.3 非線型回帰

いつも線型回帰が当てはまるとは限りません。(Anscombe 1973)の例を描画してみます。?anscombeに掲載されています。

1ff <- y ~ x
2par(mfrow = c(2, 2), mar = 0.1+c(4,4,1,1), oma =  c(0, 0, 2, 0))
for (i in 1:4){
3  ff[2:3] <- lapply(paste0(c("y", "x"), i), as.name)
  plot(ff, data=anscombe, col="red", pch=21, bg="orange",
4       xlim=c(3, 19), ylim=c(3, 13))
  abline(lm(ff, data=anscombe), col="blue")
}

1

ffに線型モデルを代入します。

2

parでパラメタを設定します。mfrowで2×2枚のパネルを作ります。余白（mar）と外部余白（oma）を設定します。下から時計回りに左、上、右の順です。

3

lapplyはリストやベクトルに函数を適用します。paste0で区切り文字なしで文字yまたはxとループの番号iを連結します。この文字列ベクトルにas.nameを適用してRのオブジェクト名にします。ffの1番目の要素には函数~()が入っているので、2番目と3番目の要素として引数を与えます。最初のループはiが1なのでy1とx2です。

4

y ~ xを最初の引数として散布図を描きます。x, yとは順序が入れ替わっているので注意が必要です。データフレームをdata=で指定します。

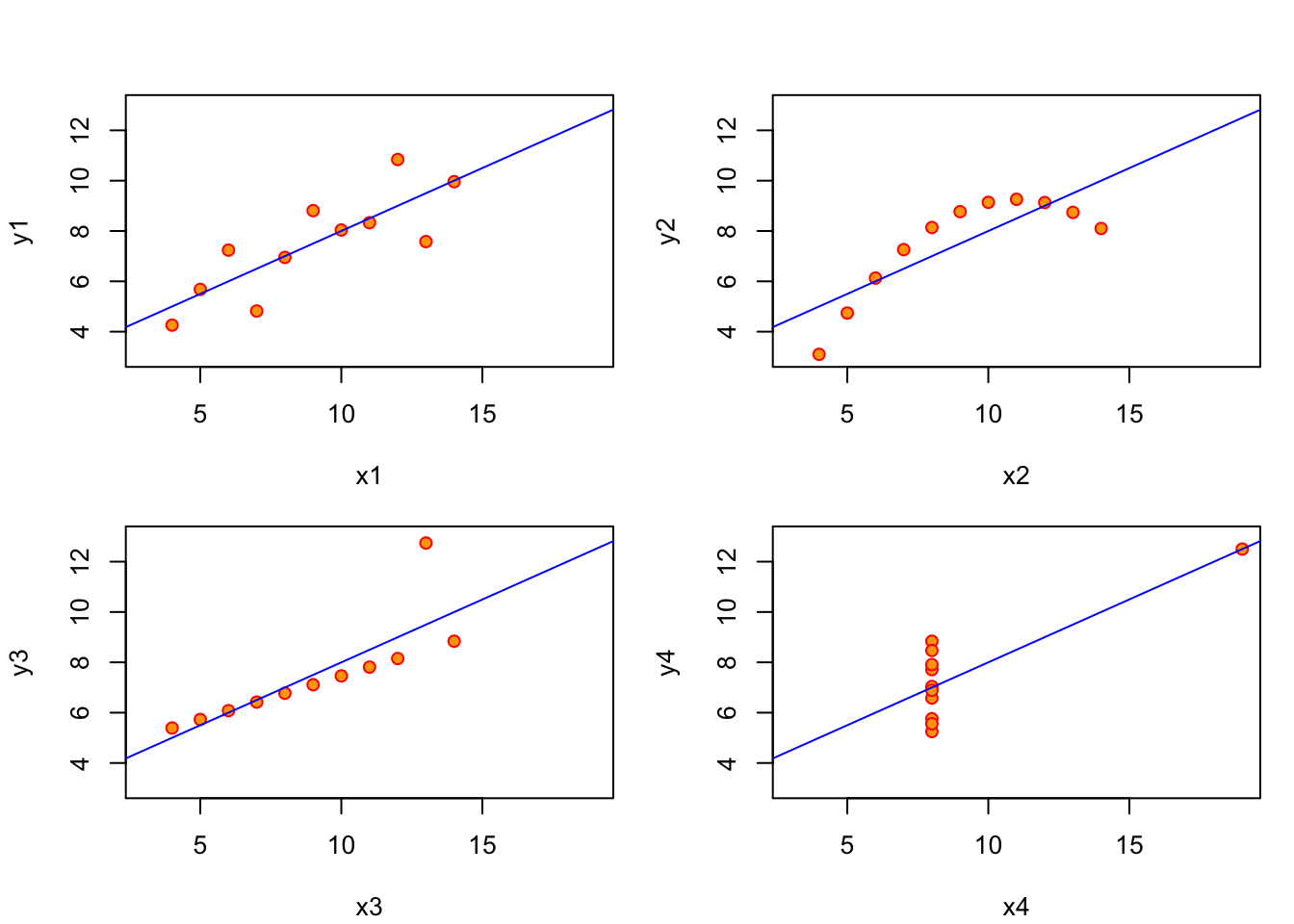
anscombの4つのデータはxの平均と分散は完全に一致し、yの平均と分散もほぼ等しいので、相関係数や回帰直線もほとんど同じです。左上は線型で良さそうです。右上は線型ではなく二次曲線の一部のように見えます。左下は外れ値の影響を受けています。右下もたった一つの外れ値のために、線型ではないのに相関係数が高くなってしまっています。統計量を計算するだけではなく、描画することが重要です。

次に 赤穂昭太郎 (2008) の例を示します。値は目分量なので、結果は教科書と同じではありません。

n <- 20
x <- seq(-2, 2, length.out=n)
y <- c(-0.18, -0.16, -0.2, -0.19, -0.18, -0.21, -0.02,
       0.31, 0.32, 0.78, 0.69, 0.4, 0.22, 0.2, -0.14,
       -0.16, -0.32, -0.4, -0.4, -0.6)
plot(x,y)
abline(lm(y ~ x))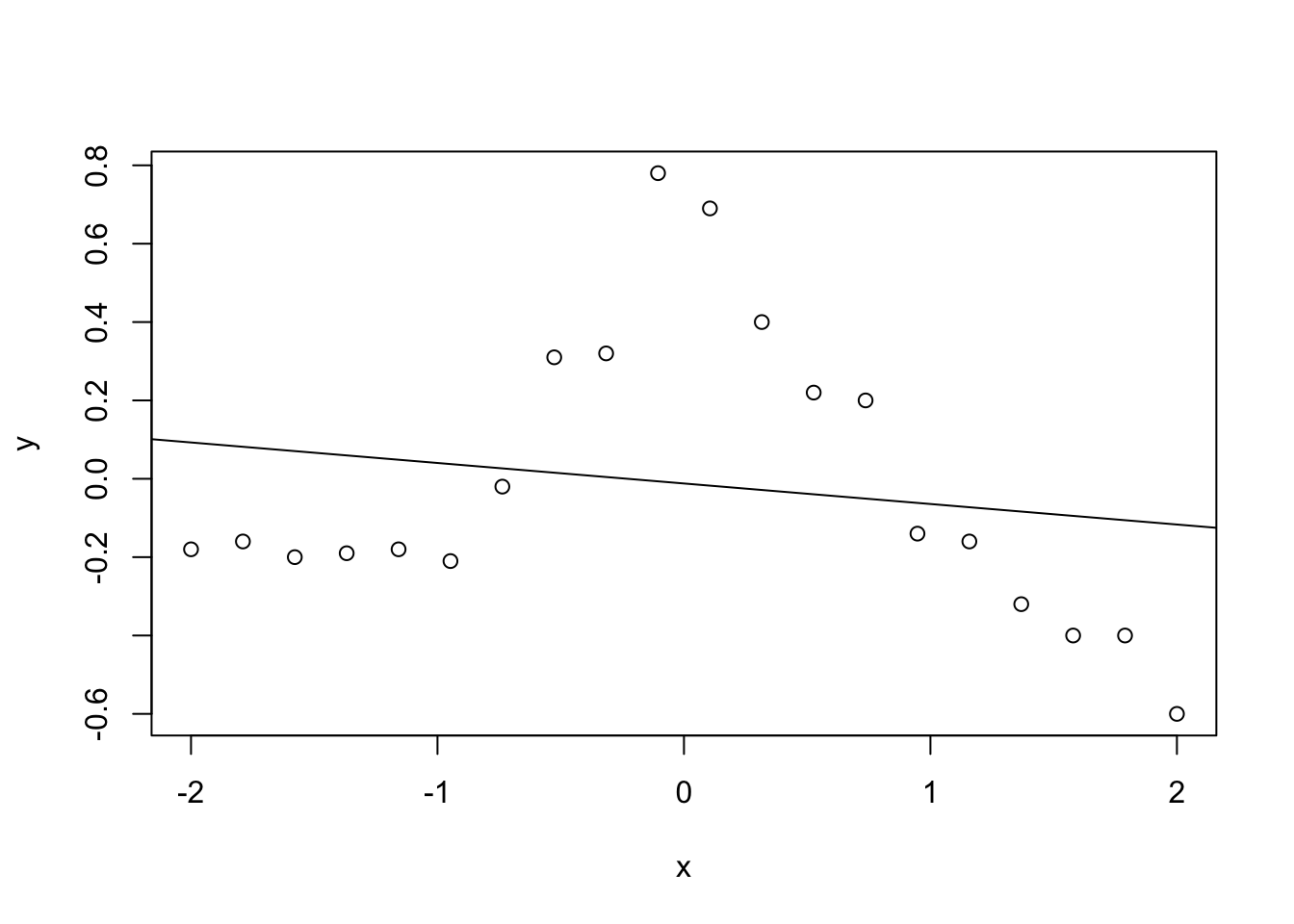

ガウス函数の線型結合

\[ f(x) = \sum_{j=1}^k\alpha_j\exp(-\beta(x_j-x)^2) \]

を用いると複雑な函数を表現できます。\(y-f(x)\)に対して最小二乗法を適用します。ただし過学習を防ぐために正則化も併用します。ガウス函数を要素とする\(k\times k\)の行列を\(\mathbf{K}\)で表します。

\[ J(\mathbf{\boldsymbol\alpha})=(\mathbf{y} - \mathbf{K}\boldsymbol\alpha)^\mathrm{T}(\mathbf{y} - \mathbf{K}\boldsymbol\alpha)+\lambda\boldsymbol\alpha^\mathrm{T}\mathbf{K}\boldsymbol\alpha \]

を最小化します。\(\mathbf{K}\)が正則であることを利用すると、重みは

\[ \boldsymbol\alpha=(\mathbf{K}+\lambda\mathbf{I})^{-1}\mathbf{y} \]

と定ります。このような手法をカーネル回帰と呼び、ここではガウス函数をカーネルとして用いました。\(\mathbf{K}\)はGram行列と呼びます。

\(\beta=1,\,\lambda=0.01\)の場合は次のようになります。

lambda <- 0.01
calc.ga <- function(x, y, beta=1.0) {
  exp(-beta * (x - y)^2)
}
x.10 <- seq(-2, 2, length.out=n*10)
kmat <- outer(x, x, calc.ga)
alpha <- solve((kmat + lambda * diag(n)), y)
y.10 <- outer(x.10, x, calc.ga) %*% alpha
plot(x, y)
lines(x.10, y.10)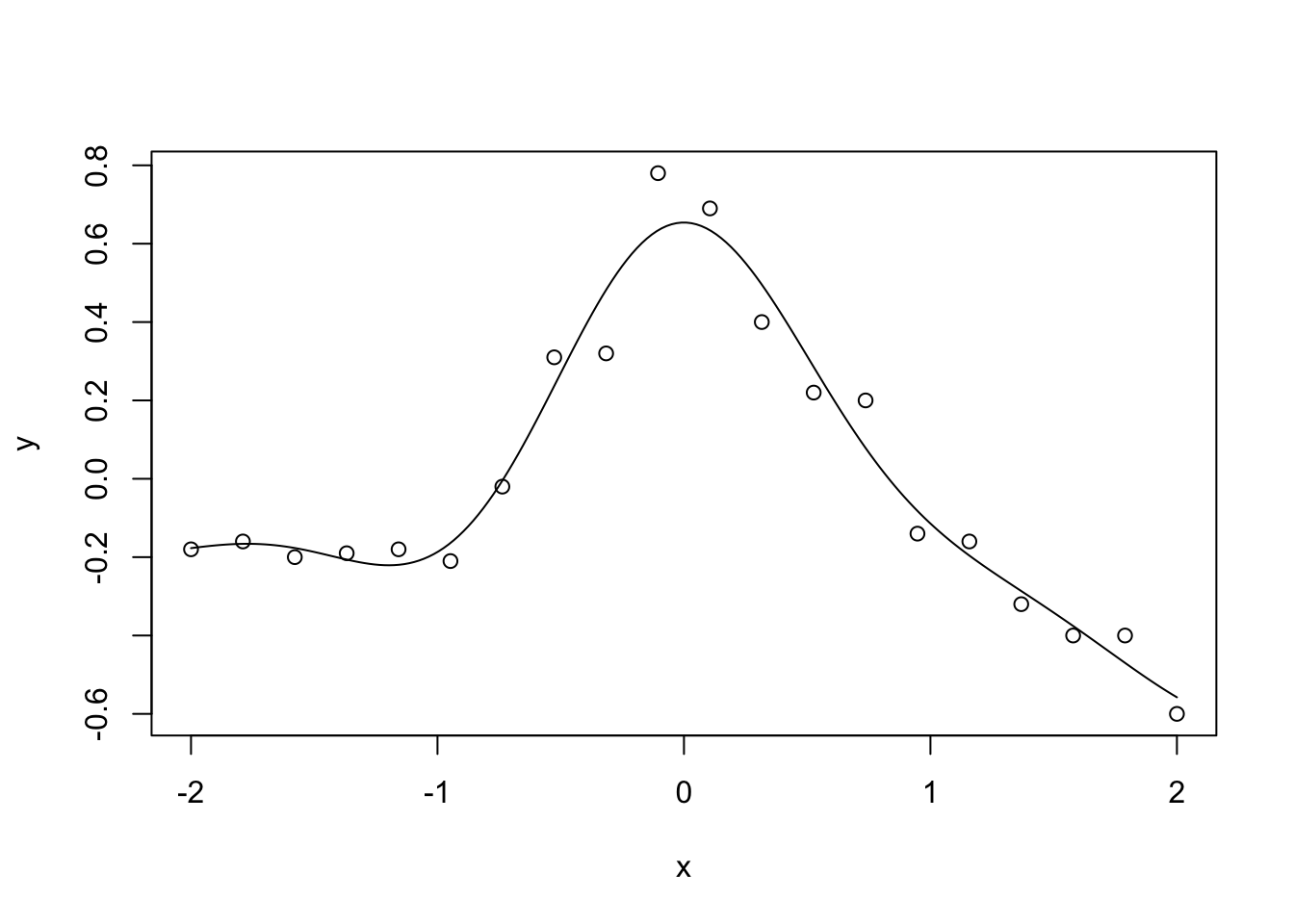

4.4 交差検証

回帰で推定された函数が一般性を持つかどうかの汎化能力を評価するため、交差検証を行なってみましょう。標本から一部を除いて学習し、除いたデータで評価を行います。これを繰り返して平均した誤差が交差検証誤差です。線型回帰やカーネル回帰の場合、データを一つずつ除く交差検証は次の式で評価できます。

\[ \mathrm{CV}=\frac{1}{n}\sum_{i=1}^k\left(\frac{y_i-\hat{y}_i}{1-H_{ii}}\right)^2 \]

ここで回帰による推定値は\(\hat{\mathbf{y}}=\mathbf{H}\mathbf{y}\)で求めます。カーネル回帰の場合\(\mathbf{H}=(\mathbf{K}+\lambda\mathbf{I})^{-1}\mathbf{K}\)です。

\(\beta=1\)に固定して\(\lambda\)を変えた場合の平均二乗誤差と交差検証誤差を求めてみましょう。

calc.mse <- function(y, yf) {
  mean((y - yf)^2)
}
calc.cv <- function(y, yf, hii){
  mean(((y - yf) / (1 - hii))^2)
}
lambda=c(1.0e-6, 0.01, 1.0)
mse=rep(0, length(lambda))
cv=rep(0, length(lambda))

i <- 1
for (l in lambda) {
  hmat <- solve((kmat + l * diag(n)), kmat)
  hii <- diag(hmat)
  alpha <- solve((kmat + l * diag(n)), y)
  yf <- outer(x, x, calc.ga) %*% alpha
  mse[i] <- calc.mse(y, yf)
  cv[i] <- calc.cv(y, yf, hii)
  i <- i + 1
}
error <- rbind(mse, cv)
rownames(error) <- c("mse", "cv")
colnames(error) <- lambda
barplot(error, beside=TRUE, legend=TRUE,
        xlab=expression(lambda), ylab="MSE/CV error")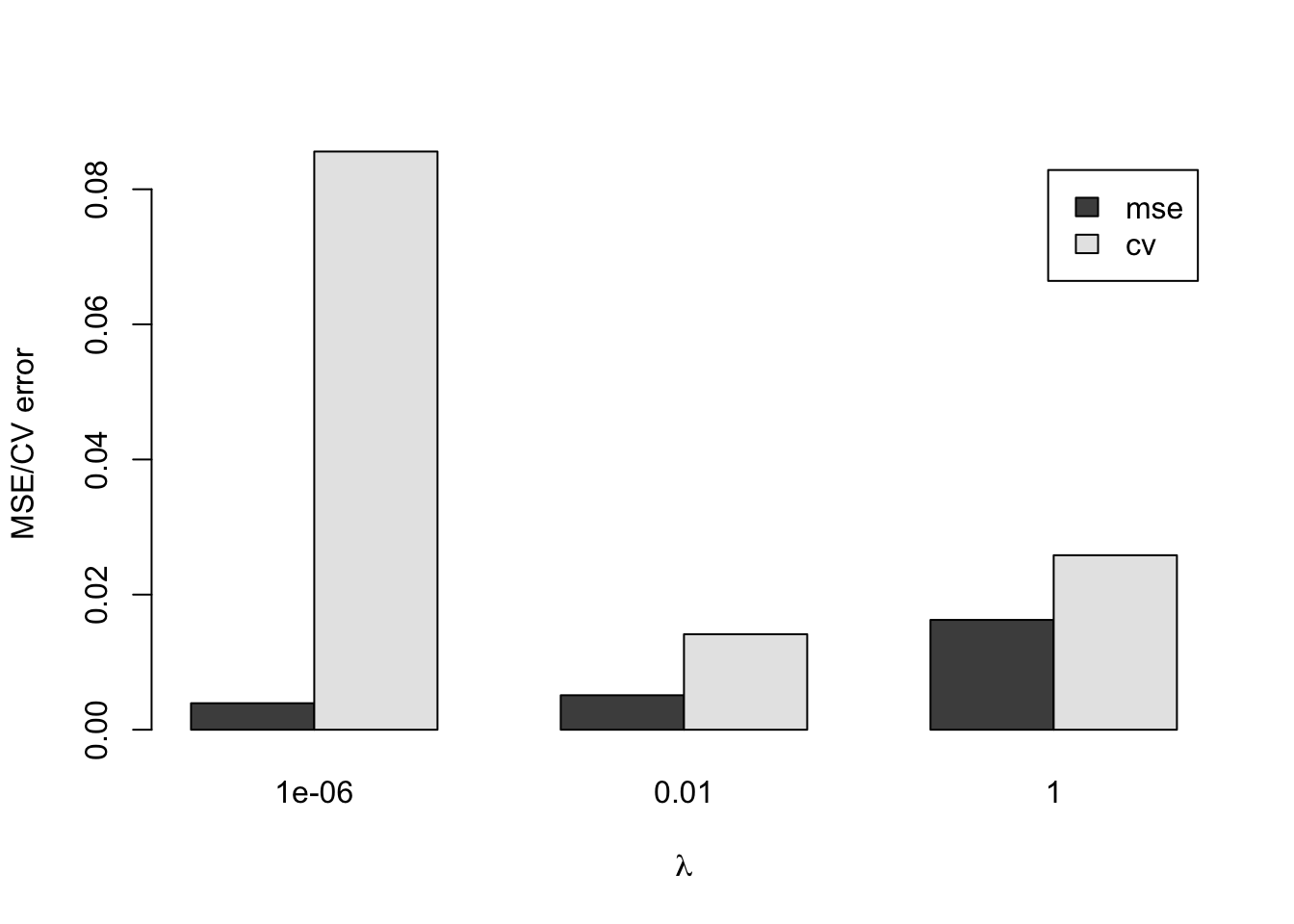

パラメタは二つの誤差が共に小さくなるように決めます。

練習

• \(\beta\)や\(\lambda\)を変えてカーネル回帰をしてみましょう。

• \(\lambda\)を固定して、\(\beta\)を変えたとき、二つの誤差を計算して教科書と比較してみましょう。

Anscombe, F. J., 1973: Graphs in Statistical Analysis. The American Statistician, 27, 17–21, https://doi.org/10.2307/2682899.

赤穂昭太郎, 2008: カーネル多変量解析―非線形データ解析の新しい展開. 岩波書店,.