l96 <- function(x, F) {
n <- length(x)
(x[c(2:n, 1)] - x[c(n-1, n, 1:(n-2))]) * x[c(n, 1:(n-1))] - x + F
}11 Lorenz-96モデル
Lorenz and Emanuel (1998) は追加の観測をどこで行うと効果的か考察するために、次の簡単なモデルを用いました。 \[ \frac{\mathrm{d}X_j}{\mathrm{d}t} = (X_{j+1} - X_{j-2})X_{j-1} - X_j + F \] \(j=1, .., J\)は格子点の番号で、\(J=40\)がよく用いられます。 格子点は緯度円上に等間隔に並んでいます。 \(X\)は気温や渦度のようなスカラーの気象学的要素を表しています。 右辺第1項は移流を表す非線型項で全エネルギー\((\sum_jX_j^2)/2\)は保存されます。 右辺第2項は消散を表す線型項で全エネルギーを減少させます。 係数が1になるようにスケールされていて、消散の時定数は5日です。 強制項\(F\)は、時空間平均\(\bar{X}\)の範囲\([0,\,F]\)、分散\(\sigma\)の範囲\([0,\,F/2]\)を決めます。 \(F>8/9\)のとき波数8の波が成長します。 このモデルの時間変化傾向はRで次のように書けます。
4次のRunge-Kutta法で時間積分をします。
rk4 <- function(f, x, dt, opts) {
k1 <- f(x, opts)
k2 <- f(x + 0.5 * dt * k1, opts)
k3 <- f(x + 0.5 * dt * k2, opts)
k4 <- f(x + dt * k3, opts)
x + (k1 + 2 * k2 + 2 * k3 + k4) * dt / 6
}\(F=3.85\)で1000ステップ先まで時間積分します。 時間刻み幅0.05は6時間に対応します。
nj <- 40
nstep <- 1001
x.hist <- matrix(0, nj, nstep)
x <- rnorm(nj)
F <- 3.85
dt <- 0.05
for (i in 1:nstep-1) {
x <- rk4(l96, x, dt, F)
x.hist[,i] <- x
}等値線を描いてみます。
t <- seq(0, nstep*dt, length.out=nstep)
filled.contour(1:nj, t, x.hist, nlevel=11,
ylim=rev(range(t)), xlab="j", ylab="time")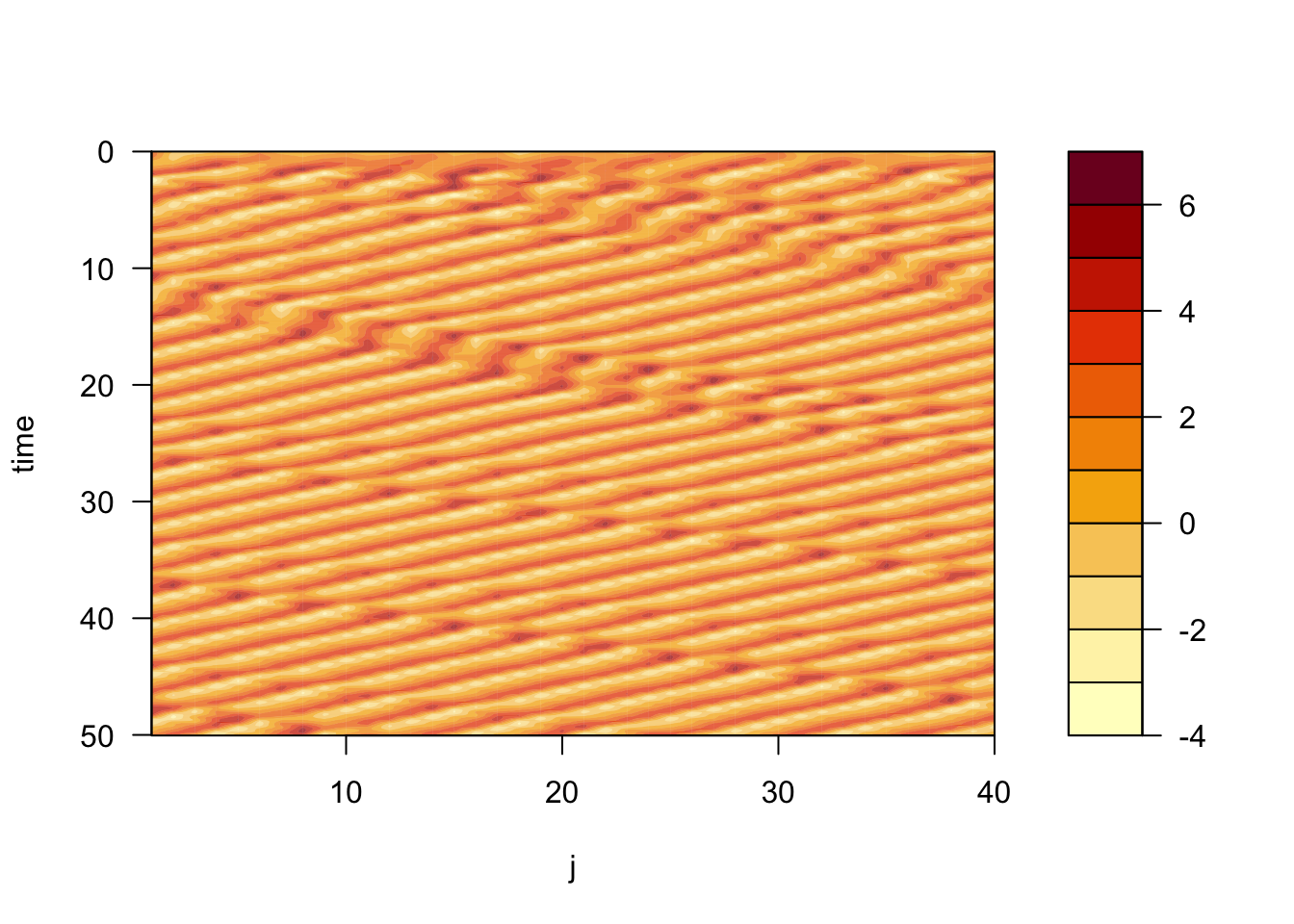
xをバイナリファイルに保存するには、writeBin()を使います。
fname <- file("l96.dat", "wb")
writeBin(x, fname)計算とは別の描画スクリプトでバイナリデータを読むにはreadBin()を使います。
nx <- 40
nstep <- 100
x <- readBin("l96.dat", double(), n=nx*nstep)縞々の数と向きから、波数は8で位相は時間とともに西に進んでいることが分かります。 これに対し初期に振幅が大きな場所は時間とともに東に進んでいます。 このようなふるまいは、定常解\(\bar{X}=F\)に対する摂動方程式の解で説明できます。 \[ \frac{\mathrm{d}x_j}{\mathrm{d}t} = (x_{j+1} - x_{j-2})F - x_j \] \(X_j=\bar{X}+x_j\)とし摂動の2次の項は無視しました。 波動解を仮定すると、\(F>8/9\)のときに波長\(L=2\pi/k=2\pi/\cos^{-1}(1/4)\approx=4.767\)の波が成長することが示されます。波長はおよそ5なので、\(J=40\)に対しては波数は8に対応します。 このとき不安定波の位相速度\(c=-(\sin k+2\sin 2k)(F/k)\)はおよそ\(-1.09\)、群速度\(c_\mathrm{g}=-(\cos k + 2\cos 2k)F\)はおよそ\(+1.17\)となります。 このほかにも不安定モードが存在しており、\(F>2.0\)では波数4から12までの波が同時に不安定に、\(F>4.0\)では波の成長で強制項の効果を打ち消すことができなくなりカオスに遷移します。 データ同化では\(F=8\)がよく用いられるようです。
- \(F\)をいろいろと変えてみましょう。
- 平均や分散が理論どおりか確認してみましょう。
- 初期摂動の影響を調べてみましょう。試行のたびに結果はどのように変わるでしょうか。