12 機械学習

PyTorchは広く使われている機械学習フレームワークです。 Torch for RはRからPyTorchのほとんどの機能が利用できます。

パッケージの名前はtorchです。 install.packages("torch")インストールしましょう。

12.1 数値最適化

Torch for Rを解説した Keydana (2023) のFunction minimization with L-BFGSに従って、数値最適化をしてみましょう。

最適化のベンチマーク函数Rosenbrock函数は \[ f(x, y) = (1-x)^2 + 100(y-x^2)^2 \] と書けます。$x$の4次函数となっており、歪んだ溝の中に最小値があります。そのため、最急降下法や共軛勾配法では、多くのステップ数を必要とします。ニュートン法やガウス・ニュートン法では、少ない回数で最小に到達することが知られています(Enomoto and Nakashita 2024)。

上記テキストでは、右辺第2項の係数が5になっていて、線型探索なしで2回、ありで1回で最適値に至るとしていますが、ここでは標準的な係数100を使います。

rosenbrock <- function(x, y, a = 1, b = 100) {
  (a - x)^2 + b * (y - x^2)^2
}

ここでは、torch for Rを使って、Rosenbrock函数を最適化します。最適化手法には、L-BFGS、線型探索には強ウルフ条件を使います。制御変数をtorchのテンソルとして定義し、初期位置を与えるとともに、勾配を自動微分で求めるためにrequries_grad=TRUEを指定します。

library(torch)

x <- torch_tensor(c(-1, -1), requires_grad = TRUE)

optimizer <- optim_lbfgs(x, line_search_fn = "strong_wolfe")

損失を計算する函数を定義します。勾配を0に初期化して、損失とその勾配を計算します。最適化の進捗を確認するため、損失を表示しています。この函数は最適化手法の1ステップoptimizer$step()に渡します。

calc_loss <- function() {
  optimizer$zero_grad()
  
  value <- rosenbrock(x[1], x[2])
  cat("value is:", as.numeric(value), "\n")
  
  value$backward()
  value
}

3ステップ数まで進み、損失をxhistに格納し、write()でテキストファイルに保存します。ファイルに格納せずに、直接描画しても構いません。

num_iterations <- 3
xhist <- as.numeric(x)
for (i in 1:num_iterations) {
  cat("\n", "iteration:", i, "\n")
  optimizer$step(calc_loss)
  cat("x=", as.numeric(x), "\n")
  xhist <- rbind(xhist, as.numeric(x))
}


 iteration: 1 
value is: 404 
value is: 62.32629 
value is: 30.0694 
value is: 2.630802 
value is: 1.178554 
value is: 1.15742 
value is: 1.132393 
value is: 1.00142 
value is: 1.091282 
value is: 0.6181912 
value is: 0.8905501 
value is: 0.6098283 
value is: 0.5655912 
value is: 0.3922533 
value is: 0.2774411 
value is: 1.417702 
value is: 0.2190705 
value is: 0.1747326 
value is: 0.1380794 
value is: 0.08087045 
value is: 0.05257415 
value is: 0.1490689 
value is: 0.0400695 
value is: 0.02954894 
value is: 0.01238139 
x= 0.9039377 0.8114879 

 iteration: 2 
value is: 0.01238139 
value is: 0.006821597 
value is: 0.002873288 
value is: 0.001204705 
value is: 0.0006028978 
value is: 4.76946e-05 
value is: 2.687239e-06 
value is: 5.929914e-08 
value is: 1.555293e-09 
value is: 3.588241e-13 
x= 0.9999999 0.9999998 

 iteration: 3 
value is: 3.588241e-13 
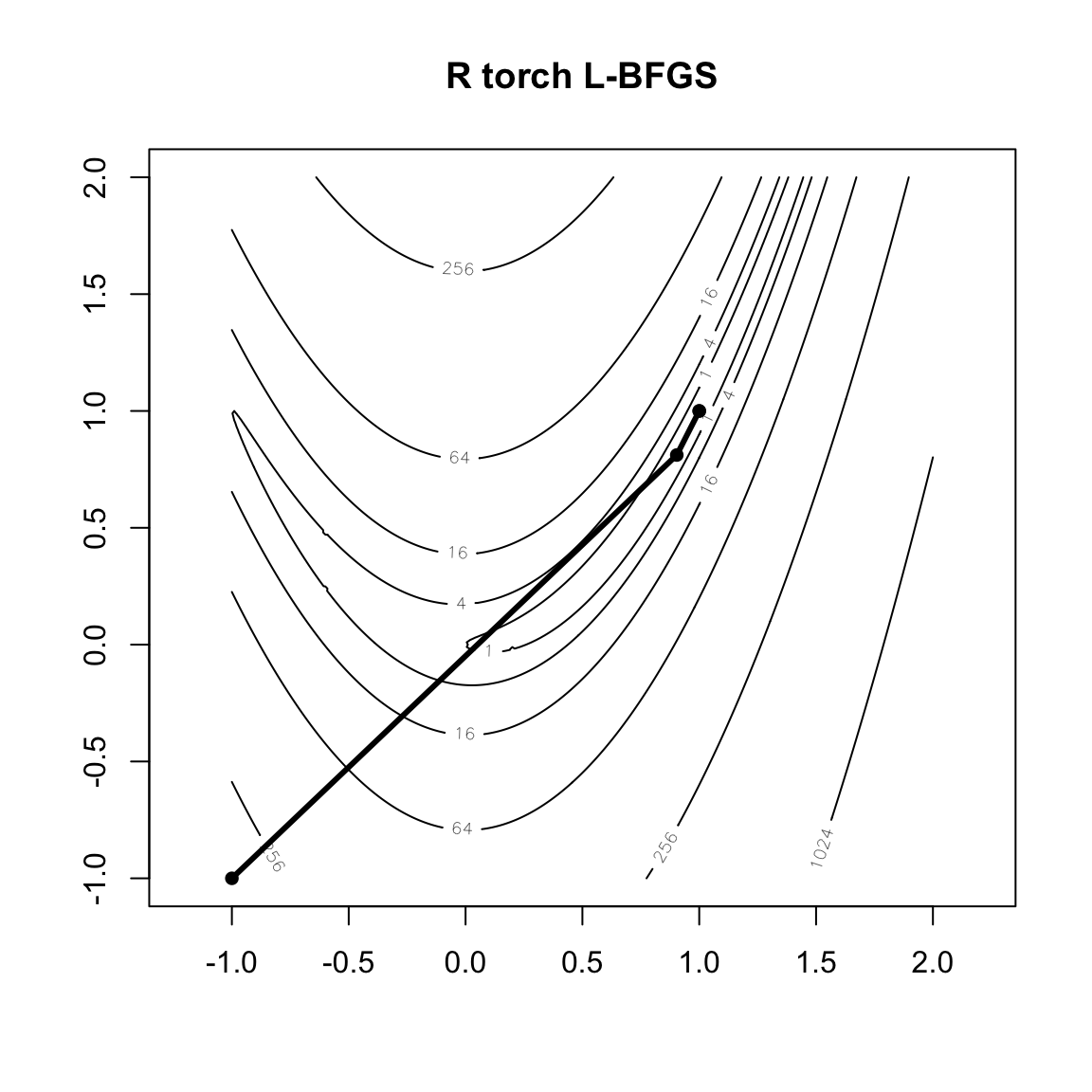
x= 0.9999999 0.9999998

write(xhist, file = "hist.txt")

2回で最小に至りました。テキストファイルに保存した最適化の履歴を読み、Rosenbrockの等値線に重ねて描画します。

xhist <- matrix(scan("hist.txt"), ncol = 2)

x.axis <- seq(-1, 2, 0.01)
y.axis <- seq(-1, 2, 0.01)
z <- outer(x.axis, y.axis, rosenbrock)

contour(x.axis, y.axis, z, levels=4^(0:10), main="R torch L-BFGS",
        asp=1, xlim=c(-1,2))
points(xhist[,1], xhist[,2], pch=16)
lines(xhist[,1], xhist[,2], lwd=3)