6 函数

ジオポテンシャル高度の定義Equation 2.1では、重力加速度は高さの函数としました。重力加速度は高さによりどのように変化するのでしょうか。重力加速度は万有引力の法則に従い、地球の中心からの距離\(a+z\)（\(a\)は地球半径）の2乗に反比例します。万有引力定数を\(G\)、地球の質量を\(M\)とすると重力加速度\(g\)は地表面からの幾何学的な高さ\(z\)の函数として、次の式で表されます。

\[ g(z) = \frac{GM}{(a+z)^2} \tag{6.1}\]

\(G=6.6743\times 10^{-11}\mathrm{m}^3\,\mathrm{kg}^{-1}\,\mathrm{s}^\mathrm{-2}\)、地球の質量を\(M=5.9742\times10^{24}\mathrm{kg}\)を使います。

6.1 重力加速度

様々な\(z\)について計算できるように、函数を作ります。Rの函数はfunctionを使って定義します。 ( )の中のzは引数と呼ばれています。 Rでは最後に評価された値が戻ります。

G <- 6.6743e-11
M <- 5.9742e24
a <- 6.371e6
calc.g <- function(z) {
  G * M / (a + z)^2
}

calc.z(0)とコンソールに入れれば地表面での重力加速度が計算できます。 g0 <- calc.z(0)とすると値がg0に入ります。 10 kmでは、100 kmではどんな値になるでしょうか。

図に描いてみましょう。

plot(calc.g, 0, 1e5, xlab="z m", ylab="g")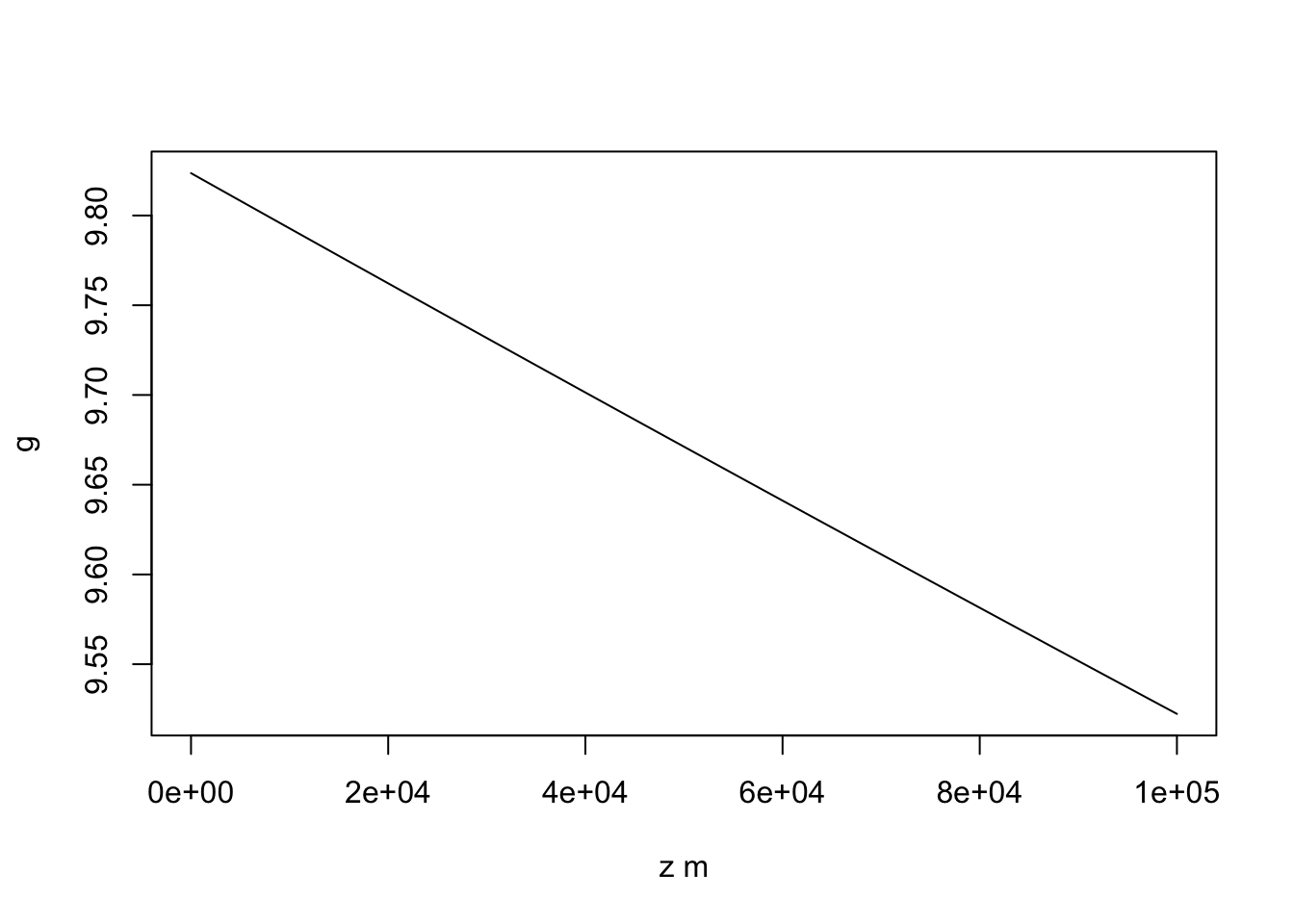

何度もコマンドを入力しなくてもいいように、以下のようなスクリプトファイルにまとめて保存しましょう。

束にまとめて一括して処理するという意味で、スクリプトを使う方法をバッチ処理と呼びます。これに対して、コンソールにコマンドをひとつひとつ入れる対話（インタラクティブ）処理と呼びます。対話処理によりデータについて調べる探索的データ分析はRの特徴ですが、その場合にも函数を書いておくと効率がよくなります。

上のコードをgravity.Rというファイルに保存してください。 sourceボタンをクリックするとスクリプトが実行され、定義した函数がコンソールで使えるようになります。

下の3行はplotGravity.Rというファイルに保存しましょう。

pdf("gravity.pdf")
plot(calc.g, 0, 1e5, xlab="z m", ylab="g")
dev.off()

plot()の前後に追加された2行について説明します。 pdf()でファイル名を指定しています。描画コマンドはdev.off()より前に描いてください。出力ファイル名を指定しない場合はRplots.pdfに出力されます。 PNG形式の場合は代わりにpng()を使います。

スクリプトはRunボタンを押すと実行されます。

6.2 幾何高度とジオポテンシャル高度

calc.gph <- function(z) {
1  integrate(calc.g, 0, z)$value / calc.g(0)
}
2z <- 0:100
3gph <- sapply(z * 1000, calc.gph) / 1000
4par(pty="s")
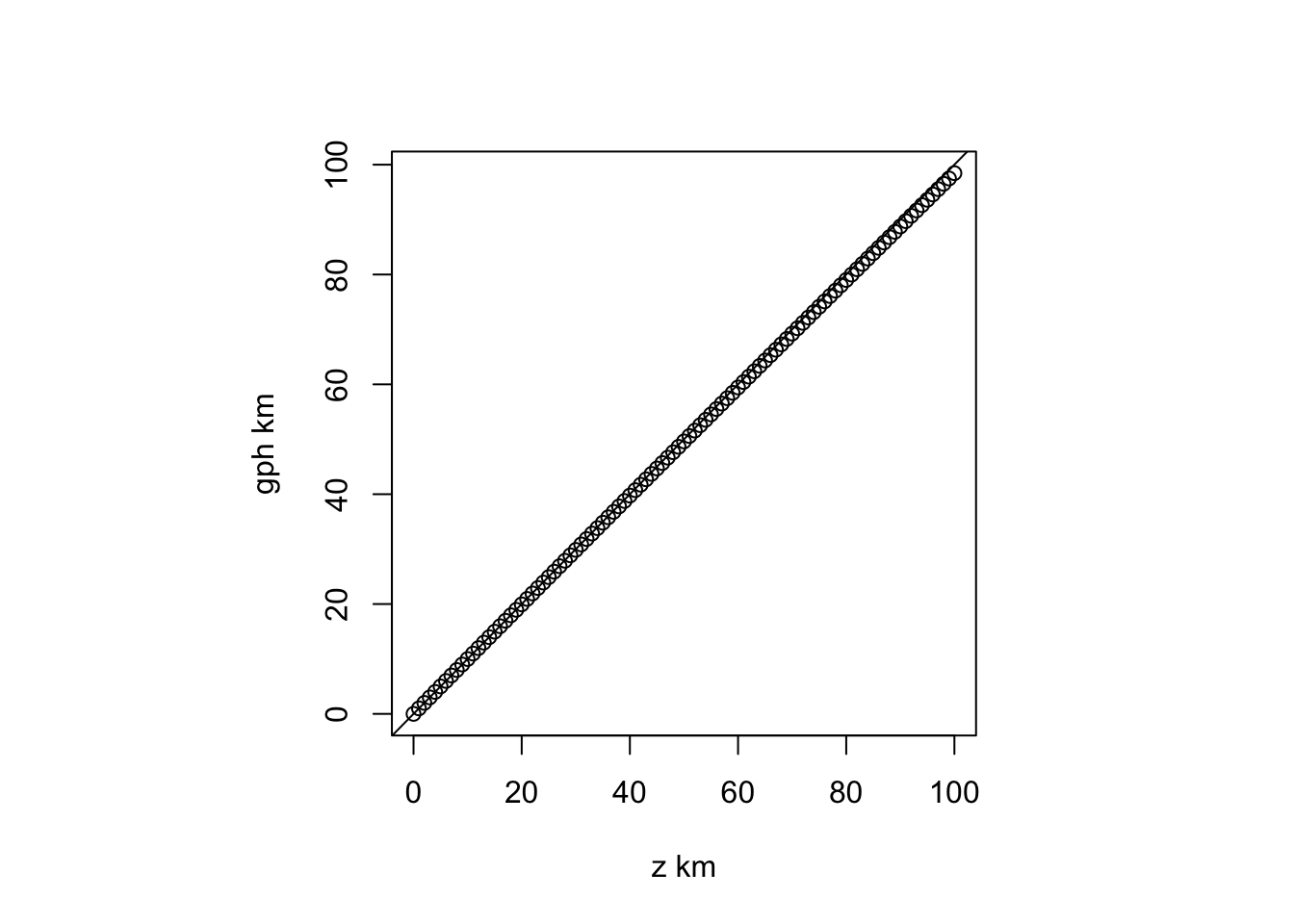
plot(z, gph, xlab="z km", ylab="gph km")
5abline(0, 1)

1: integrate()函数を使って0からzまで数値積分します。
2: 0から100まで1刻みのベクトルを作ります。
3: integrate()の積分の上限はスカラーなのでsapply()でcalc.gph()をzの各要素に作用させます。
4: 描画領域を正方形（square）にします。
5: 切片0、傾き1の直線を引きます。

練習

上記のコードをスクリプトにしてみよう。
AMeDASデータに含まれる風向16方位を角度にする函数を書いてみよう。

Code

dir2deg <- function(x) {
  dir <- seq(0, 360, length.out=17)[1:16]
  names(dir) <- c("北", "北北東", "北東", "東北東",
                  "東", "東南東", "南東", "南南東", 
                  "南", "南南西", "南西", "西南西", 
                  "西", "西北西", "北西", "北北西")
  dir[x]
}
dir <- c("北", "北北東", "北東", "東北東")
dir2deg(dir)

    北 北北東   北東 東北東 
   0.0   22.5   45.0   67.5

6.3 湿潤大気に関する函数

Bolton (1980) や世界気象機関WMO、気象庁などに基づいて、湿潤大気に関する函数を書いてみました。gistにも掲載しているほか、metに含まれています。

devtoolsをインストールして、

library(devtools)
install_github("tenomoto/mettools")

とするとインストールされます。

eps <- 0.622

e2q <- function (e, p) {
  eps*e/(p-(1.0-eps)*e)
}

q2e <- function(q, p) {
    p*q/(eps+(1.-eps)*q)
}

e2w <- function(e, p) {
    eps*e/(p-e)
}

calc.es <- function(T) {
# WMO, JMA
    exp(19.482-4303.4/(T-29.65))*100
}

calc.condtemp <- function (T, e){
#; Bolton (1980)
#; e(Pa)
    2840.0/(3.5*log(T)-log(e*0.01)-4.805)+55.0
}

ttd2q <- function(ttd, T, p) {
    e2q(calc.es(T-ttd), p)
}

rh2q <- function (rh, T, p) {
# T K, rh %
    e2q(calc.es(T)*0.01*rh, p)
}

q2ttd <- function(q, T, p) {
# WMO, JMA
  T-29.65-4303.4/(19.482-log(q2e(q,p)*0.01))
}

calc.theta <- function (T, w, p) {
# Bolton (1980)
# T(K), w(kg/kg), p(Pa)
    T*(100000.0/p)^(0.2854*(1.0-0.28*w))
}

calc.thetae <- function (T, e, p) {
# Bolton (1980)
# T(K), e(Pa), p(Pa)
    w <- e2w(e,p)
    TL <- calc.condtemp(T, e)
    calc.theta(T, w, p) * exp((3376.0/TL-2.54)*w*(1.0+0.81*w))
}

calc.thetaes <- function(T, p) {
# Bolton (1980)
# T(K), e=es(T)(Pa), p(Pa)
    es <- calc.es(T)
    w <- e2w(es,p)
    calc.theta(T, w, p) * exp((3376.0/T-2.54)*w*(1.0+0.81*w))
}