10  前線形成

冷たい空気と暖かい空気とがぶつかると気温の勾配が大きな前線ができます。初期の気温の分布が次の式で与えられているとします。\(\theta_0=290\)Kは参照温位、\(\Delta\theta\)は温位の変動幅、\(d\)は傾圧帯の幅を表します。温位は定められた気圧にしたときの気温です。傾圧帯は気温の勾配がある帯状の領域です(Keyser et al. 1988)。

\[ \theta_i=\theta_0-\frac{\Delta\theta}{2}\tanh\left(\frac{n_i}{d}\right) \]

\(n_i\)は空気塊の前線に直交する座標で気温の勾配\(\nabla\theta\)の反対向きに取ります。添え字の\(i\)は初期時刻を表しています。

\[ n_i = -x_i\sin\alpha_i + y_i\cos\alpha \]

空気がぶつかる風の場を表す流線函数は次のように表されます。

calc.pt <- function(x, y, alpha, theta0=290.0, dtheta=20.0, d=500.0) {
  n <- -x * sin(alpha) + y * cos(alpha)
  theta0 - 0.5 * dtheta * tanh(n/d)
}

\[ \psi = -bxy \]

流線函数と風とは次のような関係があります。

\[ u = -\frac{\partial\psi}{\partial y}=bx,\, v = \frac{\partial\psi}{\partial x}=-by \tag{10.1}\]

calc.psi <- function(x, y, b) {
  -b * x * y
}

風Equation 10.1を時間積分すると、空気塊の位置は時間とともに次の式で移動します。

\[ x(t) = x_ie^{bt},\,y(t)=y_ie^{-bt} \]

calc.xi <- function(x, b, t) {
  x * exp(-b * t)
}
calc.yi <- function(y, b, t) {
  y * exp(b * t)
}

南北に3200 kmの領域の設定します。

x <- seq(-1600, 1600, 100)
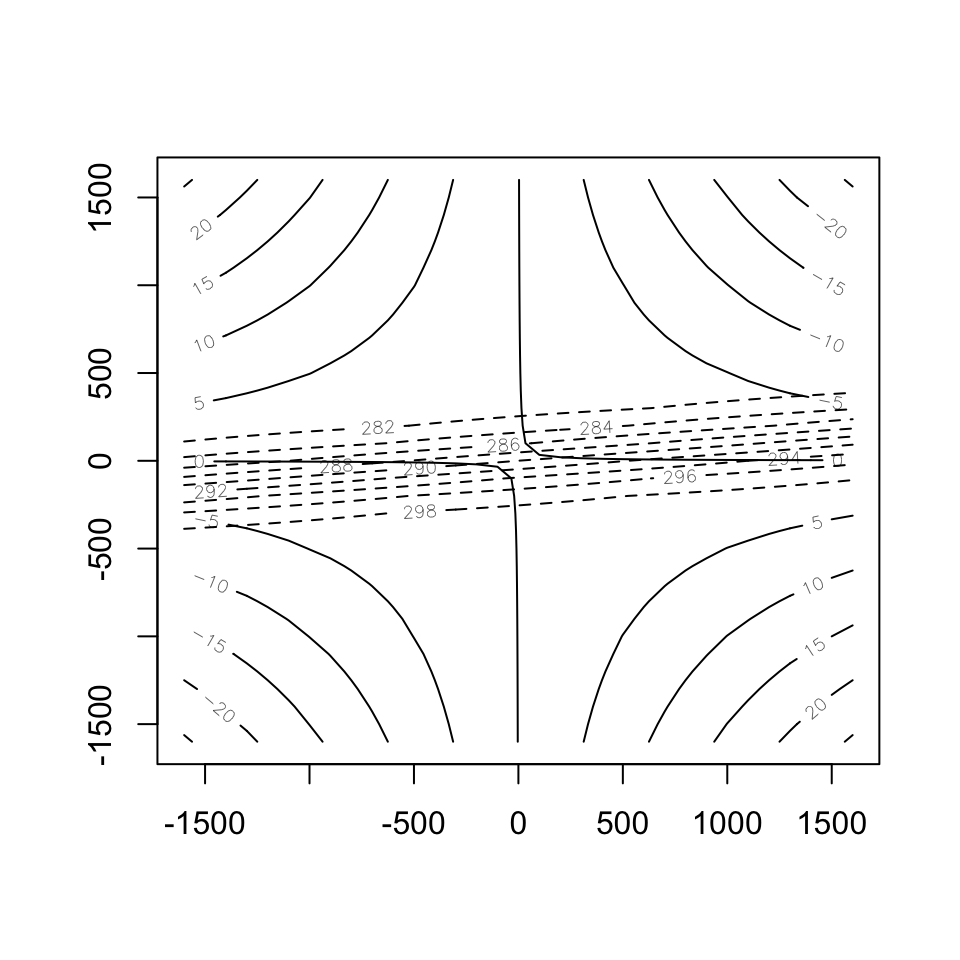
y <- seq(-1600, 1600, 100)

初期の流線函数と温位の分布は次のようになっています。

alpha <- pi / 3
b <- 1.0e-5
theta <- outer(x, y, calc.pt, alpha)
psi <- outer(x, y, calc.psi, b)
contour(x, y, psi)
contour(x, y, theta, lty=2, add=TRUE, asp=1)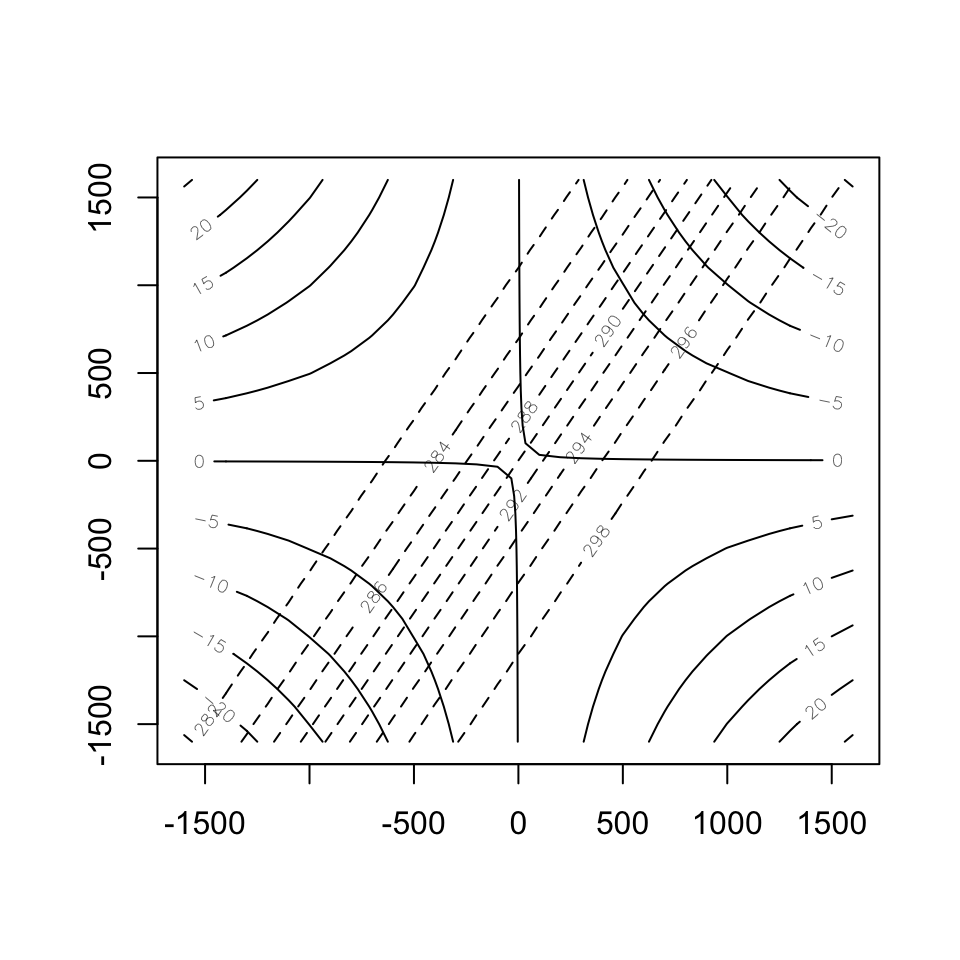

時刻 \(t=b^{-1}=27.8\) h、\(t=1.5b^{-1}=41.7\) hと時間が進むにつれて、前線は時計回りに回転しながら勾配が強化されていきます。

alpha <- pi / 3
b <- 1.0e-5
t <- 1.0 / b
theta <- outer(calc.xi(x, b, t), calc.yi(y, b, t), calc.pt, alpha)
contour(x, y, psi)
contour(x, y, theta, lty=2, add=TRUE, asp=1)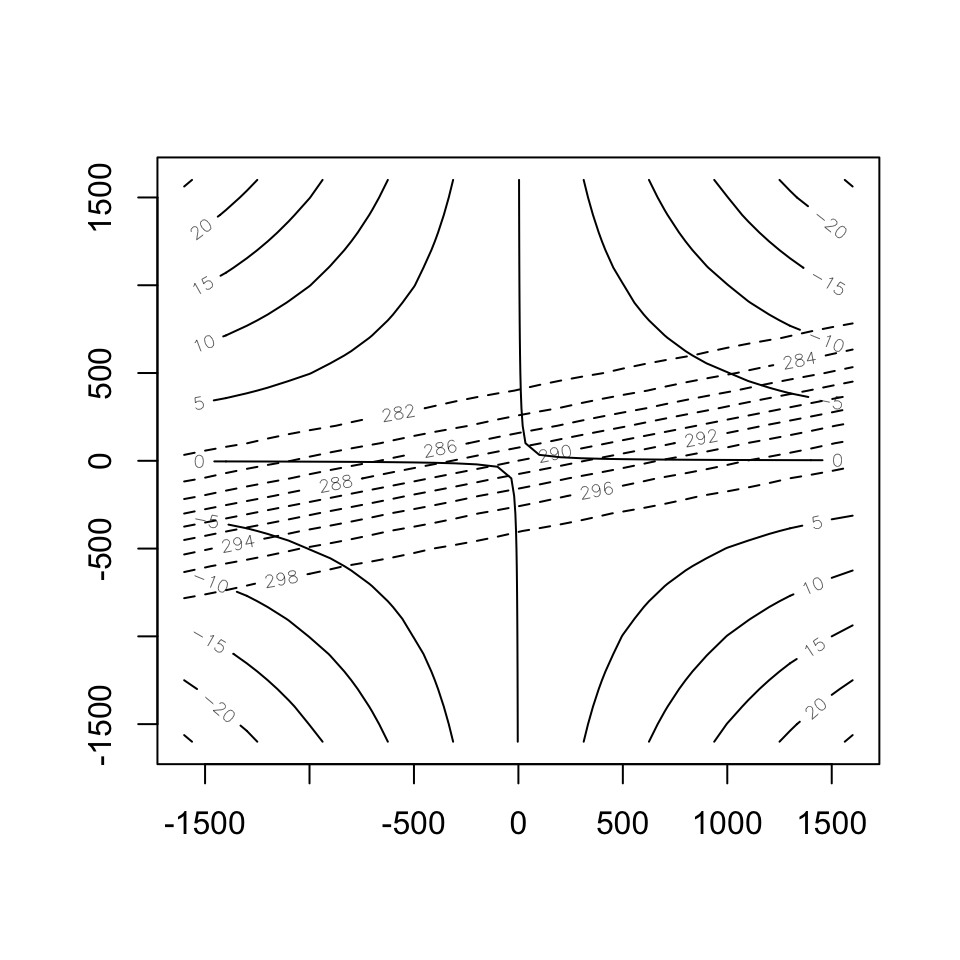

alpha <- pi / 3
b <- 1.0e-5
t <- 1.5 / b
theta <- outer(calc.xi(x, b, t), calc.yi(y, b, t), calc.pt, alpha)
contour(x, y, psi)
contour(x, y, theta, lty=2, add=TRUE, asp=1)