5 ロスビー波の伝播 – 応用気象学IA

5.1 分散関係式

線型化された準地衡渦位方程式 Equation 3.6 は

\[ \left(\frac{\partial}{\partial t} + \bar{u}\frac{\partial}{\partial x}\right)q' +\frac{\partial\bar{q}}{\partial y}\frac{\partial\psi'}{\partial x} = 0 \]

ここで

\[ q' = \nabla^2\psi' + \frac{1}{\rho_0}\frac{\partial}{\partial z^*}\left(\epsilon\rho_0\frac{\partial\psi'}{\partial z^*}\right), \]

は渦位擾乱 Equation 3.8、\(\partial \overline{q}/\partial y\)は、基本場の南北渦位勾配 Equation 3.9 である。

\(N^2\)一定、即ち\(\varepsilon\)が一定のとき、波動解

\[ \psi' = \Re\Psi e^{z/2H}e^{i(kx+ly+mz-\omega t)} \tag{5.1}\]

を Equation 3.7 、 Equation 3.8 に代入すると、分散関係式

\[ \omega = k\overline{u} - \frac{k\dfrac{\partial \overline{q}}{\partial y}}{k^2+l^2+\varepsilon\left(m^2+\dfrac{1}{4H^2}\right)} \tag{5.2}\]

が得られる。

5.2 ロスビー波の鉛直伝播

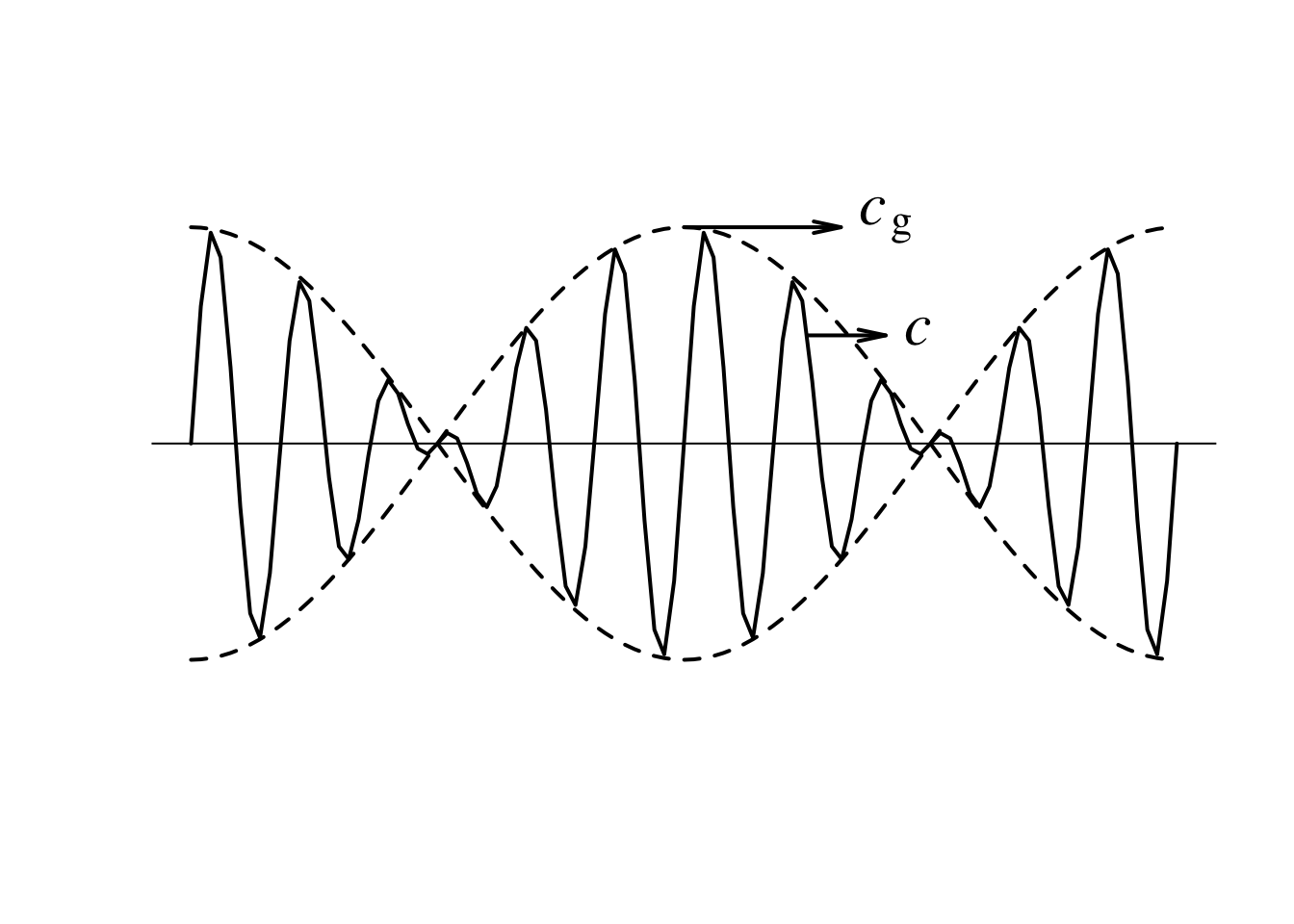
Equation 5.2 を見ると、波数により位相速度が異なることが分かる。波数の異なる波で構成されている波束は、その形が時間とともに崩れていく。このような性質を「分散性」と呼ぶ。波束が形を変えていく過程で、振幅の強め合いや弱め合いが起きるので、それぞれの波長の波の位相速度とエネルギーの伝わる速度 (群速度) とは向きや大きさが当然異なる。エネルギーの移動は、波の山谷ひとつひとつではなく、波束の輪郭の移動により表わされる Figure 5.1。

Code

k1 <- 10
k2 <- 12
eta <- function(a, k1, k2, x) {
  a * (sin(k1 * x) + sin(k2 * x))
}
env <- function(a, k1, k2, x) {
  2 * a * cos((k1 - k2) * x / 2)
}

x <- seq(0, 2 * pi, length.out = 101)
curve(eta(1, k1, k2, x), from = 0, to = 2 * pi, ylab = "", xlab = "", lwd = 2,
      axes = FALSE, ylim = c(-2.5, 2.5))
curve(env(1, k1, k2, x), from = 0, to = 2 * pi, add = TRUE, lty = 2, lwd = 2)
curve(-env(1, k1, k2, x), from = 0, to = 2 * pi, add = TRUE, lty = 2, lwd = 2)
abline(h = 0)
arrows(pi, 2, pi + 1, 2, length = 0.15, angle = 12, lwd = 2)
xc <- 1.25 * pi
arrows(xc, eta(1, k1, k2, xc), xc + 0.5, eta(1, k1, k2, xc),
       length = 0.15, angle = 12, lwd = 2)
text(pi + 1, 2, expression(italic(c)[g]), pos = 4, cex = 2, family = "Times")
text(xc + 0.5, eta(1, k1, k2, xc), expression(italic(c)), pos = 4, cex = 2, family = "Times")

Figure 5.1: 異なる2つの位相速度を持つ正弦波の重ね合わせにより作られた、連続した波束。破線は波 (実線) の包絡線を表す。

Equation 5.2 を微分して、群速度を求める。

\[ c_{\mathrm{g}y} = \frac{2\partial\overline{q}/\partial y}{\left[k^2+l^2+\varepsilon\left(m^2+\frac{1}{4H^2}\right)\right]^2}kl \tag{5.3}\]

\[ c_{\mathrm{g}z} = \frac{2\varepsilon\partial\overline{q}/\partial y}{\left[k^2+l^2+\varepsilon\left(m^2+\frac{1}{4H^2}\right)\right]^2}km \tag{5.4}\]

波動解は

\[ \psi' = \frac{\Psi}{2} e^{z/2H}(e^{i\phi}+e^{-i\phi}) \] と書ける。ここで

\[ \phi \equiv kx+ly+mz-\omega t \]

である。波動解を用いると、運動量フラックス及び熱フラックスは

\[ \overline{v'u'} = -\frac{\Psi^2}{2} e^{z/H} kl \tag{5.5}\]

\[ \overline{v'T'} =\frac{f_0H\Psi^2}{2R}e^{z/H} km \tag{5.6}\]

となる。したがって Equation 5.3, Equation 5.4, Equation 5.5, Equation 5.6 より

\[ (c_{\mathrm{g}y}, c_{\mathrm{g}z}) = \frac{4\partial\overline{q}/\partial y}{\Psi^2\left[k^2+l^2+\varepsilon\left(m^2+\frac{1}{4H^2}\right)\right]^2}(-\overline{v'u'}, \frac{f_0R}{N^2H}\overline{v'T'}) \tag{5.7}\]

が得られる。 Equation 5.7 より、Eliassen–Palmフラックス\(\pmb{F}\)の向きは局所的な群速度の向きを表すことが分かる。

5.3 ロスビー波の水平伝播

ロスビー波の水平伝播は、順圧渦度方程式で記述できる。

5.3.1 順圧渦度方程式

南北シアーを持つ基本場の東西風\(\bar{u}=\bar{u}(y)\)のまわりで線型化された順圧渦度方程式

\[ \left(\frac{\partial}{\partial t}+\bar{u}\frac{\partial}{\partial x}\right)\nabla^2\psi' + \beta_{\mathrm{eff}}\frac{\partial\psi'}{\partial x}=0 \tag{5.8}\]

を考える。ここで

\[ \beta_{\mathrm{eff}} = \frac{\partial(f+\bar{\zeta})}{\partial y}=\beta-\frac{\partial^2\bar{u}}{\partial y} \]

は実効ベータ（effective beta）と呼ばれる。

\(x, y\)方向に波動解を仮定して、分散関係を求める。波動解を

\[ \psi'=\Re \hat{\psi}\exp i(kx+ly-\omega t) \]

とし、 Equation 5.8 に代入すると、分散関係式

\[ \omega = k\overline{u}-\frac{k\beta_{\mathrm{eff}}}{k^2+l^2} \tag{5.9}\]

を得る。

5.4 ロスビー波の西進

Equation 5.9 を\(k\)で割って東向きの位相速度\(c_x\)を求めると、

\[ c_x-\overline{u} = -\frac{\beta_{\mathrm{eff}}}{k^2+l^2} < 0 \]

が得られる。東西風に相対的な位相速度\(c_x-\overline{u}\)は負なので、ロスビー波は西進する。

Equation 5.9 を\(k,l\)で微分して、\(x\) 方向の群速度 \(c_{\mathrm{g}x}\), \(y\)方向の群速度\(c_{\mathrm{g}y}\)を求める。 \[ c _{\mathrm{g}x} = \overline{u} - \frac{\beta_{\mathrm{eff}}[l^2-k^2]}{[k^2+l^2]^2} \tag{5.10}\]

\[ c _{\mathrm{g}y} = \frac{2kl\beta_{\mathrm{eff}}}{[k^2+l^2]^2} \tag{5.11}\]

を得る。東西風に相対的な東西位相速度 \(c_{x}-\bar{u}\) が常に負であったのに対し、波の形状 (\(k, l\)) により、東西風に相対的な東西群速度は西向きにも東向きにもなりうる。

5.5 定常ロスビー波

位相速度\(c_x=0\)のとき

\[ \overline{u} = \frac{\beta_{\mathrm{eff}}}{k_{\mathrm{s}}^{2}} \]

が成り立つ。このようなロスビー波を定常ロスビー波と呼ぶ。ここで

\[ k_{\mathrm{s}}^{2} \equiv k^{2} + l^{2} = \frac{\beta_{\mathrm{eff}}}{\bar{u}} \tag{5.12}\]

を定常ロスビー波数と呼ぶ。これを Equation 5.10, Equation 5.11 に代入すると,

\[ \pmb{c}_\mathrm{g} = 2\overline{u}% \begin{pmatrix} k \\ l \end{pmatrix} \frac{k}{k_{\mathrm{s}}^{2}} \tag{5.13}\]

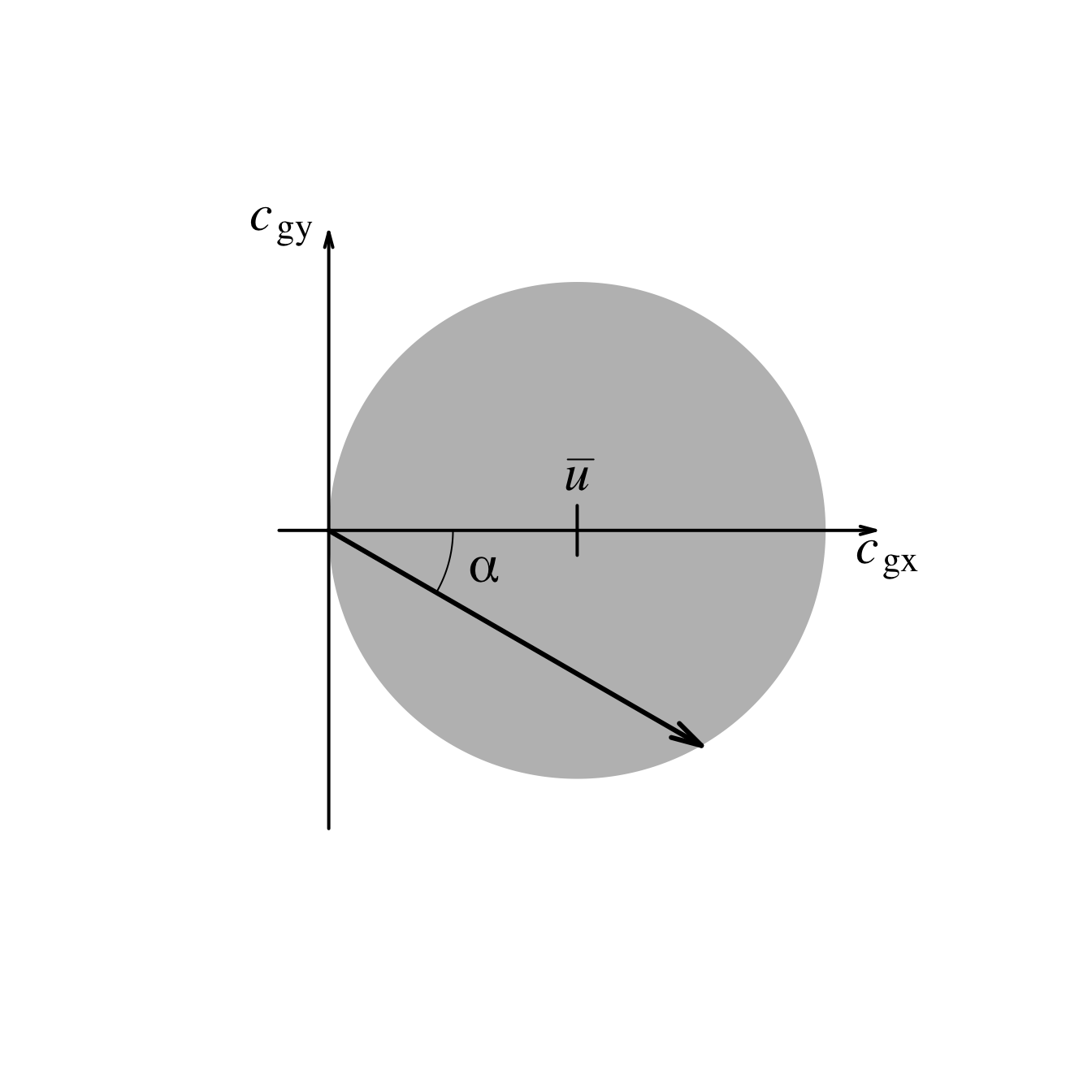
となる。定常ロスビー波の向きは常に東向きで、 \(x\) 軸方向（東向き）に伝播するとき \(|\pmb{c}_\mathrm{g}|\)は最大値\(2\overline{u}\) を取ることが分かる。

Code

theta <- 0:360 * pi / 180
plot(cos(theta), sin(theta), type = "n", axes = FALSE, asp = 1,
     xlim = c(-1.5, 1.5), ylim = c(-1.5, 1.5), xlab = "", ylab ="")
polygon(cos(theta), sin(theta), col = "gray", border = NA)
arrows(-1, -1.2, -1, 1.2, length = 0.1, angle = 15, lwd = 2)
arrows(-1.2, 0, 1.2, 0, length = 0.1, angle = 15, lwd = 2)
alpha <- -pi / 6
segments(0, -0.1, 0, 0.1, lwd = 2)
arrows(-1, 0, cos(2 * alpha), sin(2 * alpha),
       length = 0.2, angle = 15, lwd = 3)
text(0, 0.1, expression(bar(italic(u))), pos = 3, cex = 2, family = "Times")
text(1.25, 0, expression(italic(c)[gx]), pos = 1, cex = 2, family = "Times")
text(-1, 1.2, expression(italic(c)[gy]), pos = 2, cex = 2, family = "Times")
text(-0.5, -0.16, "α", pos = 4, cex = 2, family = "Times")
theta1 <- -30:0 * pi /180
lines(0.5 * cos(theta1) - 1, 0.5 * sin(theta1))

定常ロスビー波の伝播は、Snellの法則に従う光波に類似している (Hoskins and Ambrizzi 1993)。式 Equation 5.13 は

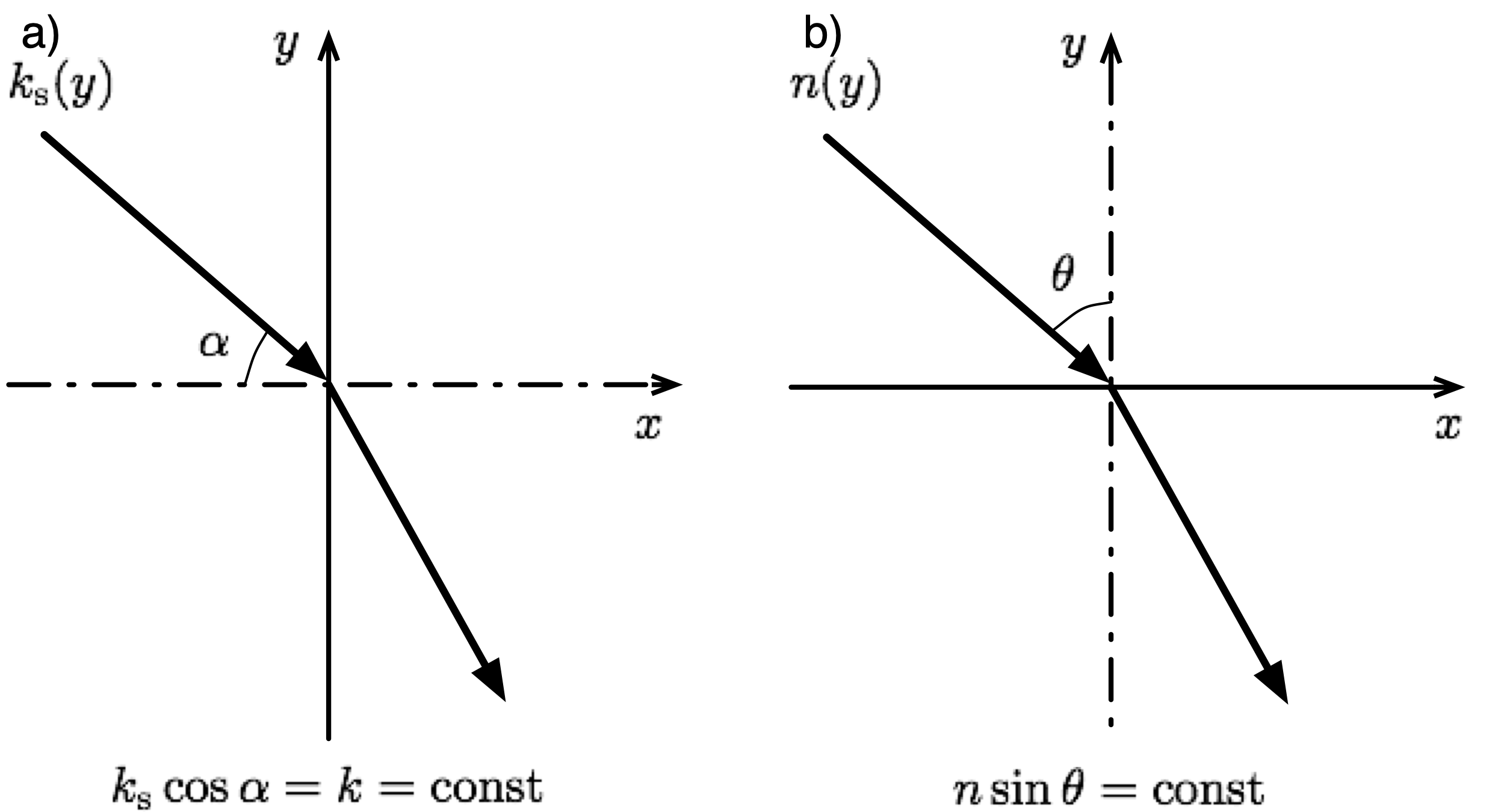
\[ \begin{aligned} \pmb{c}_\mathrm{g} &= 2\overline{u} \begin{pmatrix} \dfrac{k}{k_{\mathrm{s}}} \\ \dfrac{l}{k_{\mathrm{s}}} \end{pmatrix} \frac{k}{k_{\mathrm{s}}} \\ &= 2\overline{u} \begin{pmatrix} \hat{k} \\ \hat{l} \end{pmatrix} \cos\alpha \end{aligned} \] と書ける。\((\hat{k},\hat{l})は\)単位ベクトルなので、波は\(x\)軸に対して\(\alpha\)の角度で伝播することが分かる。 \(\cos\alpha\)の定義より

\[ k = k_\mathrm{s}\cos\alpha = \mathrm{const} \tag{5.14}\]

と書ける。

これは、屈折率\(n\), \(y\)軸に対する角度\(\theta\)で伝播する光波について成り立つ Snell の法則

\[ n\sin\theta = \mathrm{const} \tag{5.15}\]

と同形である。式 Equation 5.14 と Equation 5.15 とを比較すると、定常ロスビー波数 \(k_\mathrm{s}\)が屈折率に相当することが分かる。

Figure 5.3: (a) ロスビー波の伝播と (b) 光波の伝播との類比。

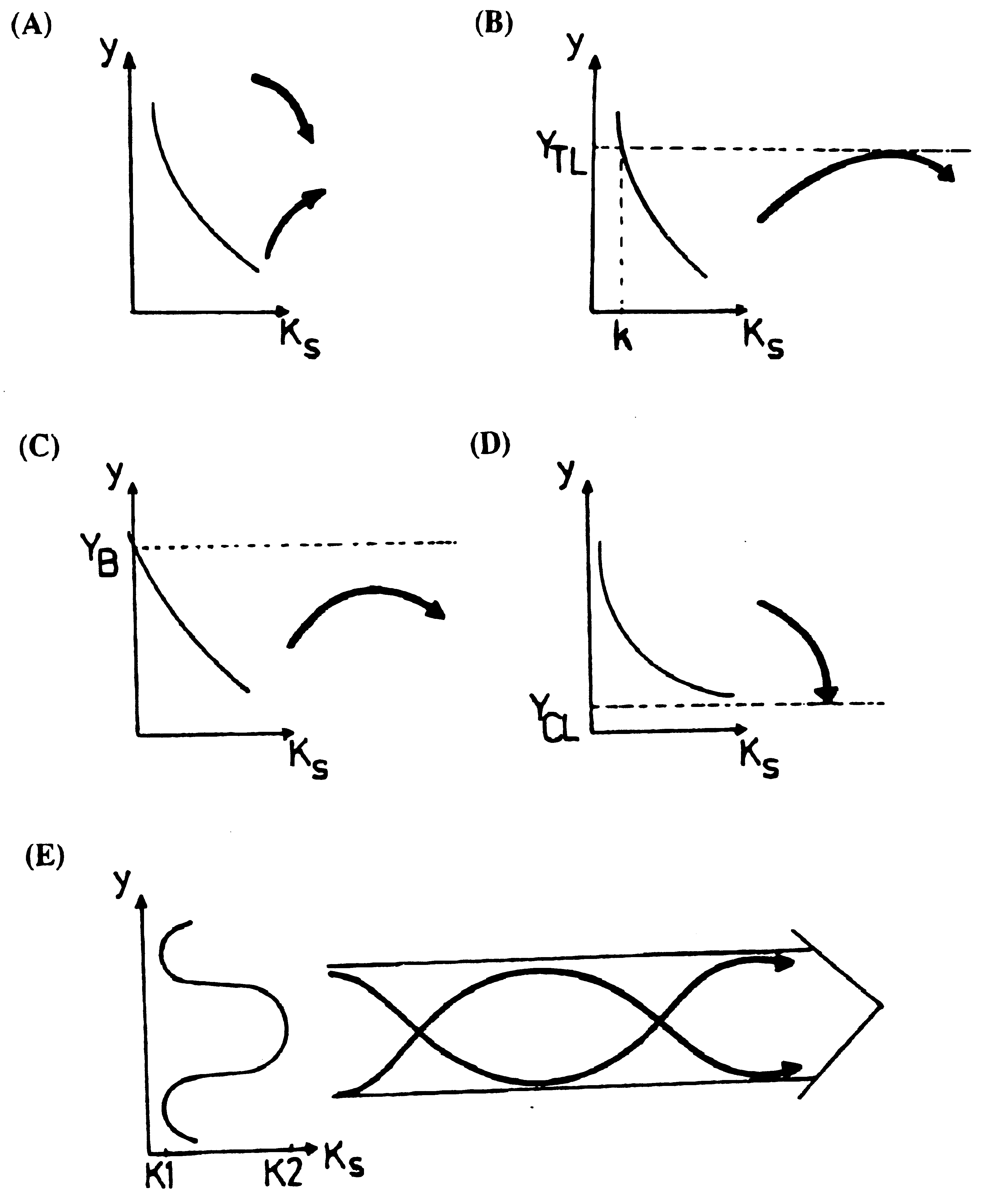
光波同様、定常ロスビー波も \(k_{\mathrm{s}}\) の大きなところに向かって伝播する (Fermat の原理, Figure 5.4A)。 \(k_{\mathrm{s}}\) の極大があれば、そこに捕捉される (Figure 5.4 E)。このように「鋭い」偏西風は、「導波管」と呼ばれる。

Figure 5.4: 定常ロスビー波の屈折や反射 (Hoskins and Ambrizzi 1993) (A) 屈折、 (B) 転移緯度での反射、 (C) 実効ベータが0となる緯度での反射、 (D) 臨界緯度での吸収、 (E) ジェット気流によるロスビー波の捕捉。

Figure 5.5: 南半球冬季における帯状平均 (a) 東西風速 (m,s\(^{-1}\)) 及び (b) 定常ロスビー波数 \(k_{\mathrm{s}}\) の南北分布(James 1994)。

式 Equation 5.12 を\(l\)について解くと,

\[ l = \pm\sqrt{k_{\mathrm{s}}^{2}-k^{2}} \]

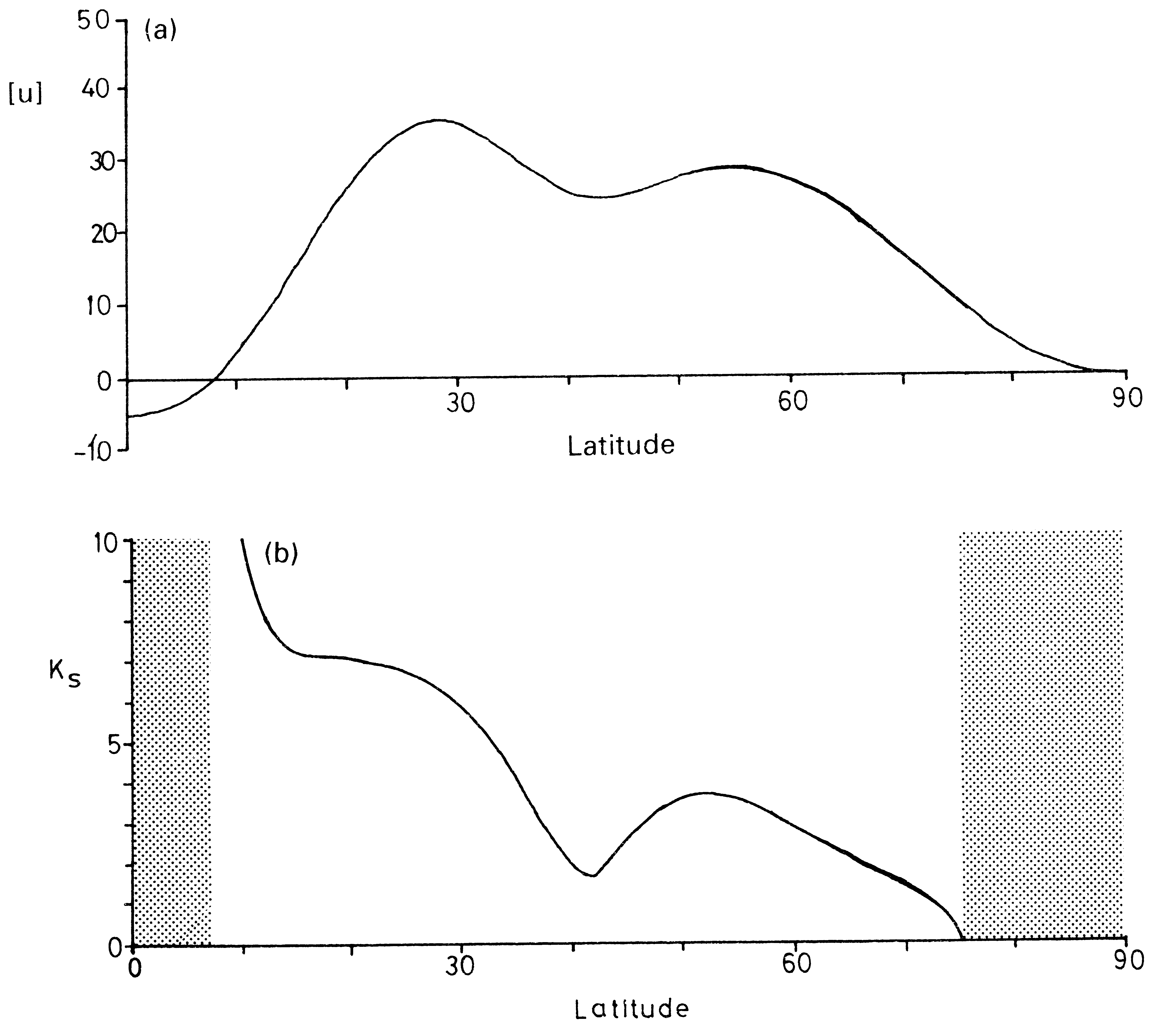
となる。 \(l>0\)のとき北向き、\(l<0\)のとき南向き伝播を表す. 通常対流圏上層では、\(k_{\mathrm{s}}\)は中緯度から亜熱帯に向かって増加している Figure 5.5。高緯度に向かって\(k_{\mathrm{s}}\)が減少して、\(k=k_{\mathrm{s}}\)となる緯度を転移緯度（turning latitude)と呼ぶ。転移緯度より極よりでは、振幅が指数函数的に減少 (evanescent) する。転移緯度では、\(l\)が符号を変え、波の向きが変わるため、波は低緯度に反射される（Figure 5.4 B）。実効ベータが負になる領域も波の反射板（reflector）として働く（Figure 5.4 C）。一方、赤道付近に東風域と中緯度の西風との間に \(\bar{u}=0\) となる緯度（臨界緯度 critical latitude）が存在する。臨界緯度に近づくと、式 Equation 5.12 から明らかなように、\(k_{\mathrm{s}}\) が急速に大きくなる。臨界緯度は定常ロスビー波の「ブラックホール」である (Figure 5.4 D)。

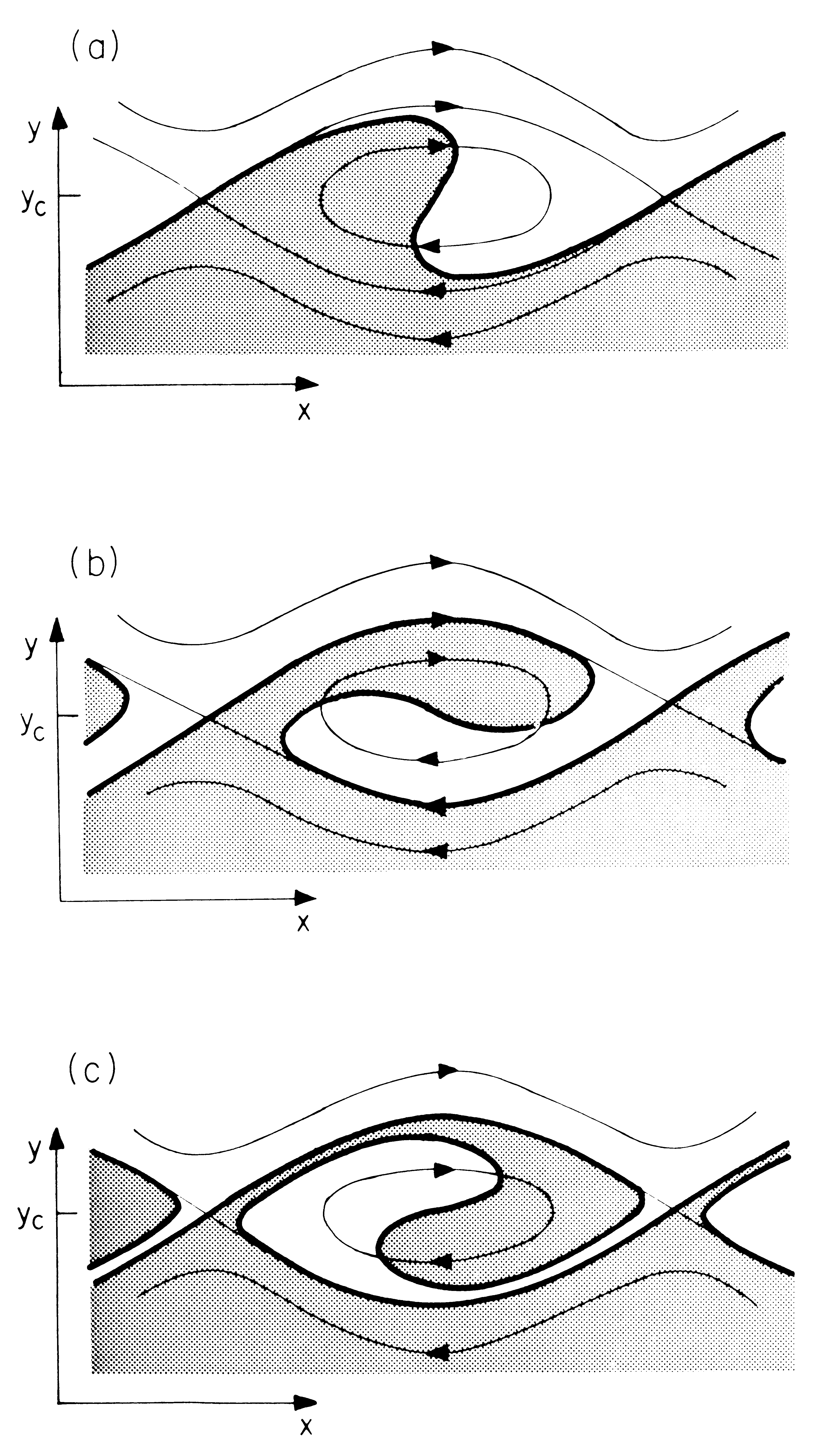
非線型性を考慮すると、波は臨界緯度付近の南北に狭い領域で、進む向きが逆転して反射されることが示されている (Figure 5.6） SWW Stewartson (1977), Warn and Warn (1978) 解)。 SWW解は、Kelvin の猫目 (cat’s eye) と呼ばれる流れのパターンである。

Figure 5.6: 臨界緯度付近での SWW Warn and Warn (1978) 解の模式図 (Andrews et al. 1987)。

5.6 北半球冬季・夏季の導波管

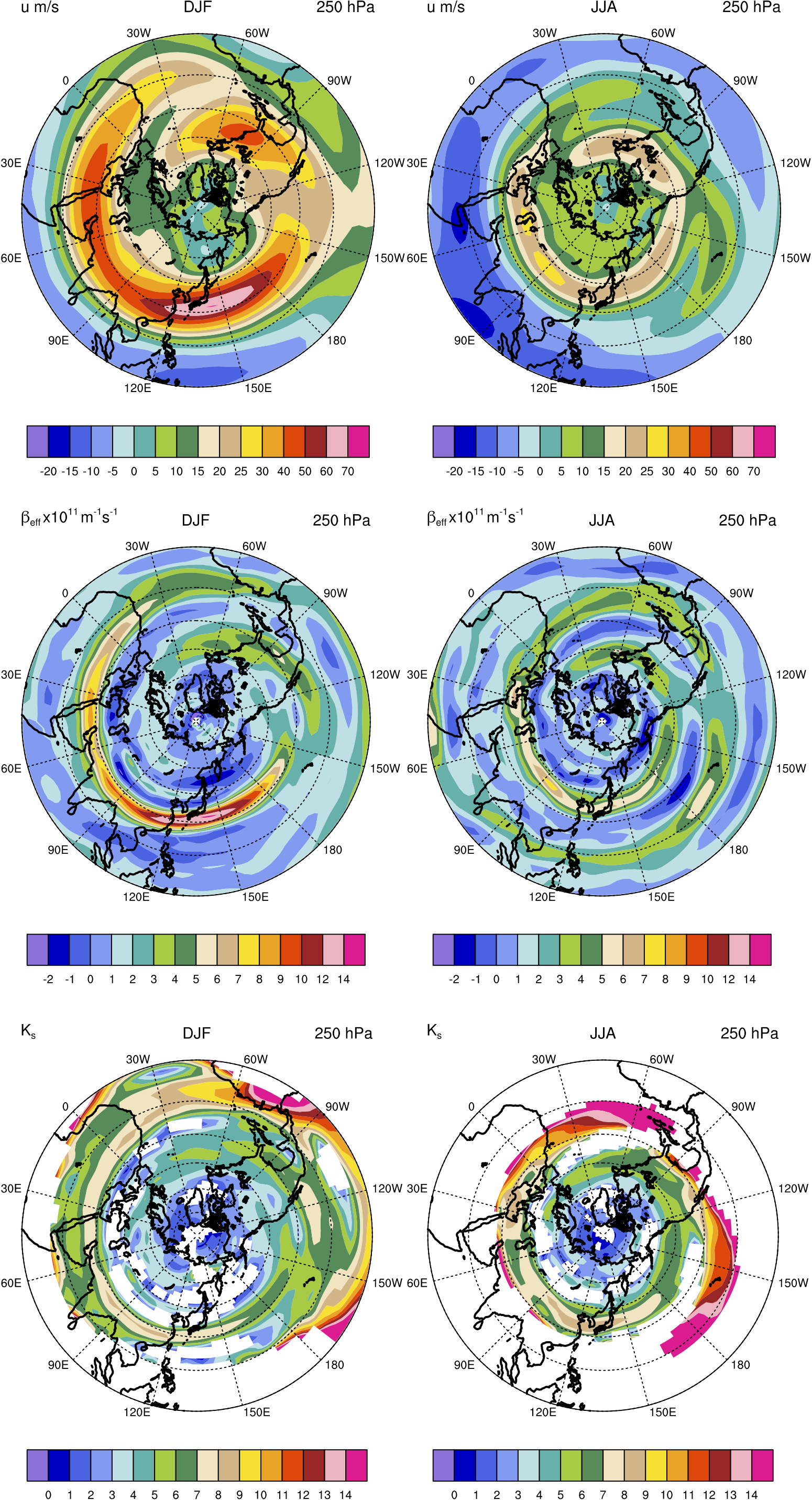
ここでは、北半球対流圏上部における定常ロスビー波の気候学的な通り道を調べておこうFigure 5.7。

北半球冬季には、日本付近と北米東岸に東西風の極大がある。 \(\beta_{\mathrm{eff}}\) で見ると、極大の南北両側で負となる領域がある。このような領域は、 Figure 5.4 Eのような導波管の構造をしている。太平洋東部には、 \(k_{\mathrm{s}}\) の大きな領域が赤道まで伸びている。この領域は西風ダクト (westerly duct) と呼ばれており、両半球の間でエネルギー交換が行われると考えられている。エルニーニョ等の年々変動により、西風ダクトが出来ない年もある。

北半球夏季には、チベット高気圧の北縁に東西風の極大が存在している。風速は、冬季ほど大きくはないが、\(k_{\mathrm{s}}\) では同程度の大きさである。値は小さいが、北極海沿岸にも波の伝播可能域が存在することも注目に値する。太平洋の導波管は、亜熱帯から伸び、北大西洋の導波管につながり、北太平洋の導波管は、亜寒帯ジェットに伴う北極海沿岸に連なる渦巻き構造をしている。

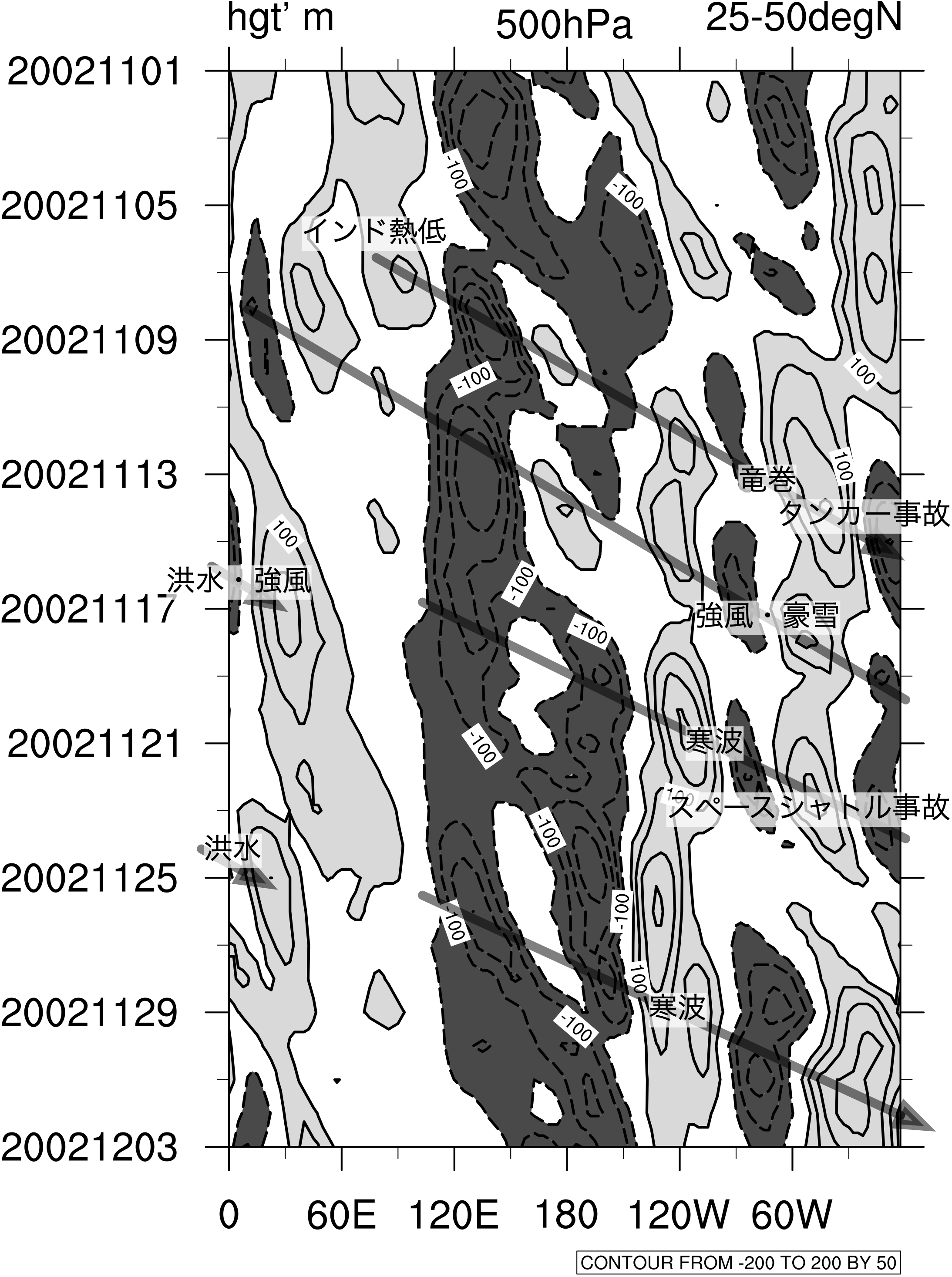
Figure 5.7: NCEP/NCAR再解析 Kalnay et al. (1996) 気候値 (1968–1996年の各季節を平均して作成) から作成した上から東西風、有効ベータ、定常ロスビー波波数。左列は12, 1, 2月平均、右列は6, 7, 8月平均。

定常ロスビー波束が異常気象の連鎖をもたらした例を Figure 5.8 に示す。

Figure 5.8: 2002 年11 月の500 hPa 面ジオポテンシャル高度の東西偏差(等値線間隔50 m) の時間–経度断面図．25–50\(^\circ\)N 平均。NCEP–NCAR 再解析 Kalnay et al. (1996) 日平均データから作成

課題

以下のいずれかの課題を一つ選び簡潔にまとめよ。

この1年間に日本に接近した顕著な温帯低気圧について、その発達過程を線型不安定論と比較せよ。
昨冬（去年の12月〜今年の2月）の平均の東西平均された東西風、南北風、運動量フラックス、熱フラックス、EPフラックスを描画し、気候値との違いについて述べよ。
今年の梅雨入りと梅雨明けの予想を検証せよ。また、アジア・ジェット上の定常ロスビー波の活動について調べ、梅雨明けとの関係について議論せよ。