台風が北極まで到達することは,まず考えられません。台風を北極に置いた座標系を考えると中心付近の構造を調べるのに便利なことがあります。経度が方位角,余緯度が台風中心からの距離を表し,接線風は東西風,動径風は南北風で表されます。
はじめに
台風中心を北極として0.5度刻みに80度まで点を打ってみます。緯度円一周には100点あります。変な呼び方ですが,軸を傾けて台風の中心を北極とした座標系を「北極座標系」と呼ぶことにします。
デカルト座標系
経度\(\lambda\), 余緯度\(\theta\)(\(90度 – 緯度\))と地球の中心を原点としたデカルト座標系の位置ベクトル \(\bm{r}=(x, y, z)^\mathrm{T}\) とは次のような関係があります。
\[
x = \cos\lambda\sin\theta \\
y = \sin\lambda\sin\theta \\
z = \cos\theta
\]
回転行列
先ほどの点の緯度経度を求めてみましょう。北極が台風の中心\((\lambda_\mathrm{c}, \theta_\mathrm{c})\)に移動するようには,次の二つの回転を組み合わせます。
- \(y\)軸の周りに\(-\theta_\mathrm{c}\)回します。この回転は,\(x\)–\(z\)平面で時計回り,すなわち負となることに注意。
- \(z\)軸の周りに\(\lambda_\mathrm{c}\)回します。
最初の回転は
\[
\mathrm{A}_1 =
\begin{pmatrix}
\cos\theta_\mathrm{c} & 0 & \sin\theta\mathrm{c} \\
0 & 1 & 0 \\
-\sin\theta_\mathrm{c} & 0 & \cos\theta_\mathrm{c}
\end{pmatrix}
\]
もう一つは
\[
\mathrm{A}_2 =
\begin{pmatrix}
\cos\lambda_\mathrm{c} & -\sin\lambda_\mathrm{c} & 0 \\
\sin\lambda_\mathrm{c} & \cos\lambda_\mathrm{c} & 0 \\
0 & 0 & 1
\end{pmatrix}
\]
と行列で表すことができます。これらを作用される順序に注意して合成すると
\[
\mathrm{A}=\mathrm{A}_2\mathrm{A}_1=\begin{pmatrix}
\cos\lambda_\mathrm{c}\cos\theta_\mathrm{c} & -\sin\lambda_\mathrm{c} & \cos\lambda_\mathrm{c}\sin\theta_\mathrm{c} \\
\sin\lambda_\mathrm{c}\cos\theta_\mathrm{c} & \cos\lambda_\mathrm{c} & \sin\lambda_\mathrm{c}\sin\theta_\mathrm{c} \\
-\sin\theta_\mathrm{c} & 0 & \cos\theta_\mathrm{c}
\end{pmatrix}
\]
となります。
なお,このような回転は大円回転として知られており,合成図解析で使われていることをJAMSTECの山崎哲さんにご教示いただきました(例えば,Nakamura et al. 1997やYamazaki 2011)。
天文では,傾いた座標が「黄道座標系」に対応します。台風の中心から反時計回りに90度の位置に春分点があります。ここでは\(y\)軸の周りの回転を考えましたが,大円回転は\(x\)軸の周りの回転です。
スカラー場
海面気圧のようなスカラー場の内挿値を求めるには,次のようにします。
- 北極の周りに上の図に示したような北極座標上の点を決めます。
- それらを式(1)を使ってデカルト座標で表します。
- 行列(4)を作用させて緯度経度を求めます。\(\mathrm{A}\bm{r}\)
- その緯度経度で値を内挿します。
ベクトル場
風のようなベクトル場は,北極座標系で見たときの向きで表す必要があります。先ほどは台風の周りにとった位置ベクトルを回転しました。ここでは,座標系を回転するので回転行列は\(\mathrm{A^T}=\mathrm{A}_1\mathrm{A}_2\)をベクトルに作用させます。
水平風をデカルト座標系で表すと次のようになります。
\[
\dot{x} = -u\sin\lambda – v\cos\lambda\cos\theta \\
\dot{y} = u\cos\lambda – v\sin\lambda\cos\theta \\
\dot{z} = v\sin\theta
\]
デカルト座標の風を緯度経度座標に戻すには
\[
u = \dot{y}\cos\lambda – \dot{x}\sin\lambda \\
v = -(\dot{x}\cos\lambda + \dot{y}\sin\lambda)\cos\theta + \dot{z}\sin\theta
\]
を使います。
風の変換手順は次のようになります。
- 水平風を式(5)を使ってデカルト座標に直します。
- \(\dot{x},\, \dot{y},\,\dot{z}\)それぞれをスカラーと見て内挿します。
- 座標を回転する。\(\mathrm{A^T}\dot{\bm{x}}\)
- 式(6)で緯度経度座標に戻します。このときの経度\(\lambda\)と余緯度\(\theta\)は北極座標系の値を使います。
2012年台風第16号
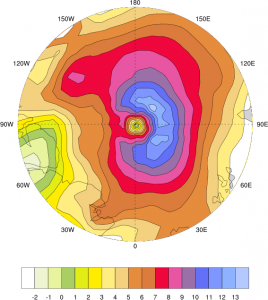
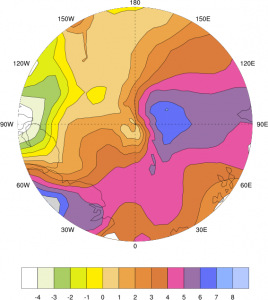
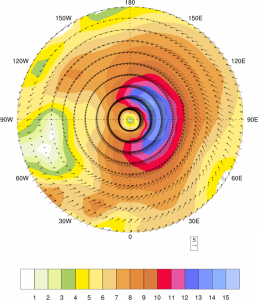
それでは実際に変換した例を見てみましょう。2012年9月14日00UTCに台風第16号は900 hPaまで強まりました。このときのALERA2の10 m風は次のようになっていました。
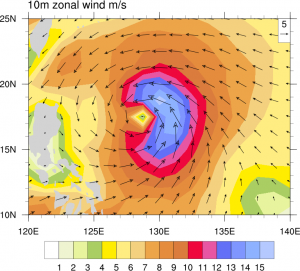
北緯17.5度,東経128.5度を北極とする座標系を考え,内挿・座標変換すると次のようになりました。
接線風
動径風
風速の絶対値とベクトル
変換のスクリプトはgistで公開しています。
変更履歴
- 2020/11/25 北極座標系で北極に点を配置した場合,\(v\)に不連続が生じるため,\(w\)を含めた3次元の風の座標変換における\(v\)を求める式に変更しました。中下さんの指摘。
- 2020/11/26 \(w\ne0\)を考えなくても\(\dot{x}\cos\lambda + \dot{y}\sin\lambda = -v\cos\theta\)と\(\dot{z}=v\sin\theta\)から\(v\)の式が求められるので水平風に戻しました。